ZKW 线段树半学习半发明笔记

图片看不清的可以在这里下载矢量图。

前言

ZKW 线段树由清华大学张昆玮在 2011 年发明。

网络上讲述 ZKW 的文章少，讲得明白的又是少之又少，因此整个 ZKW 线段树我都是半学半发明的，可能跟原本 ZKW 的想法不一样，但一定是对的（AC 证明 :D）

概述

ZKW 线段树不需要递归，常数极小，空间是普通线段树的一半。比较好写。可能比较好理解。

ZKW 线段树是自底向上维护的。

由于 ZKW 线段树可以使用懒标记（网上一堆说不可以打标记的，包括某谷的日报）

堆式存储

ZKW 线段树的存储方式跟普通线段树的存储方式差异很小，都是堆式存储。

所谓堆式存储，就是按照左儿子为 $2x$，右儿子为 $2x + 1$，父亲为 $\lfloor x/2\rfloor$ 的方式进行存储。

ZKW 线段树要求建出来的树一定要是满二叉树（加一堆空节点硬凑）。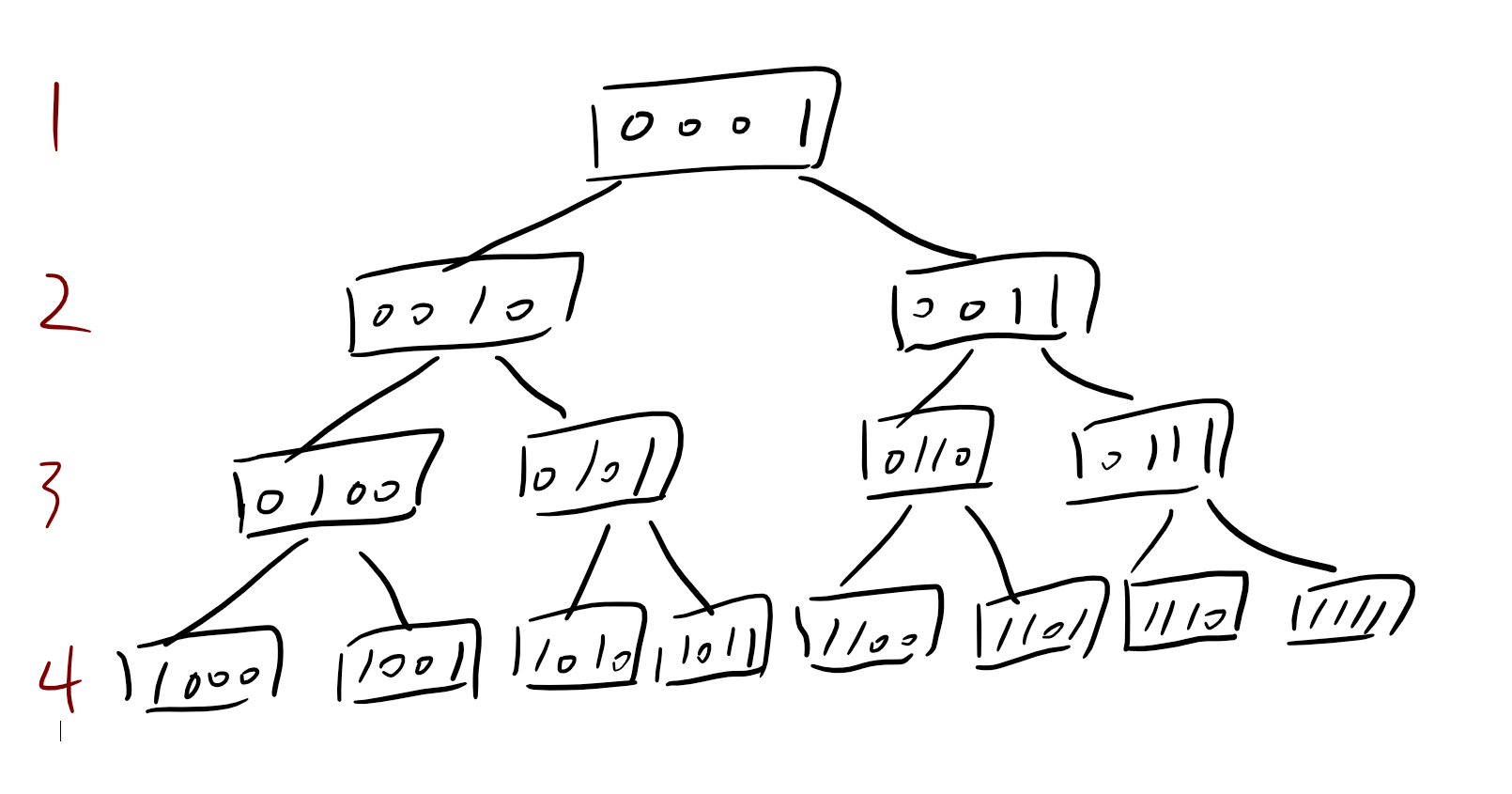

仔细看一眼，发现很像字典树！再看一眼，发现叶子节点就是原数组上的节点，而相应的，我们也可以通过这种方式快速从原数组对应到线段树上的节点。

建树

for (P = 1; P + 1 <= n; P *= 2);
vector<tp> a(P << 1), t(P << 1);  // a 是维护的信息，t 是永久化的标记
--P;
for (tp i = 1; i <= n; ++i) bin >> a[i + P];
for (tp i = P; i; --i) a[i] = a[i << 1] + a[i << 1 | 1];

单点操作

自底向上维护。首先找到要修改的位置在线段树上的位置，然后暴力跳父亲更新信息。

auto update = [&](tp x, tp d) -> void {
  for (tp i = x + P; i; i /= 2) a[i] += d;
};

区间操作

区间操作比较巧妙。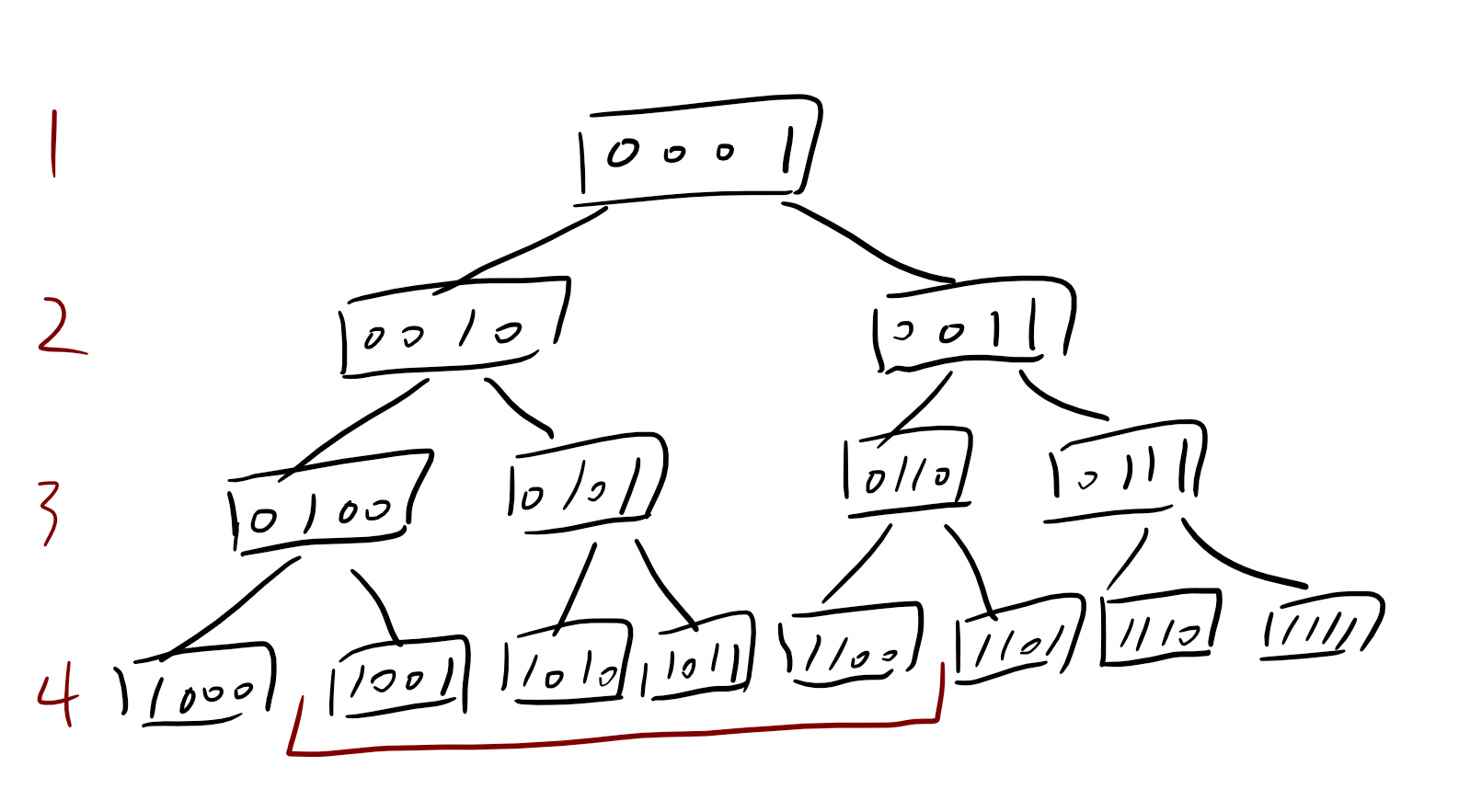

假设我们要操作的是我框出的这一段。

首先，确定出左端点的左边的那个点 和 右端点右边的那个点（图中打叉的点），相当于是变成开区间（当然，这意味着我们可能要浪费掉最左边和最右边的这两个点）。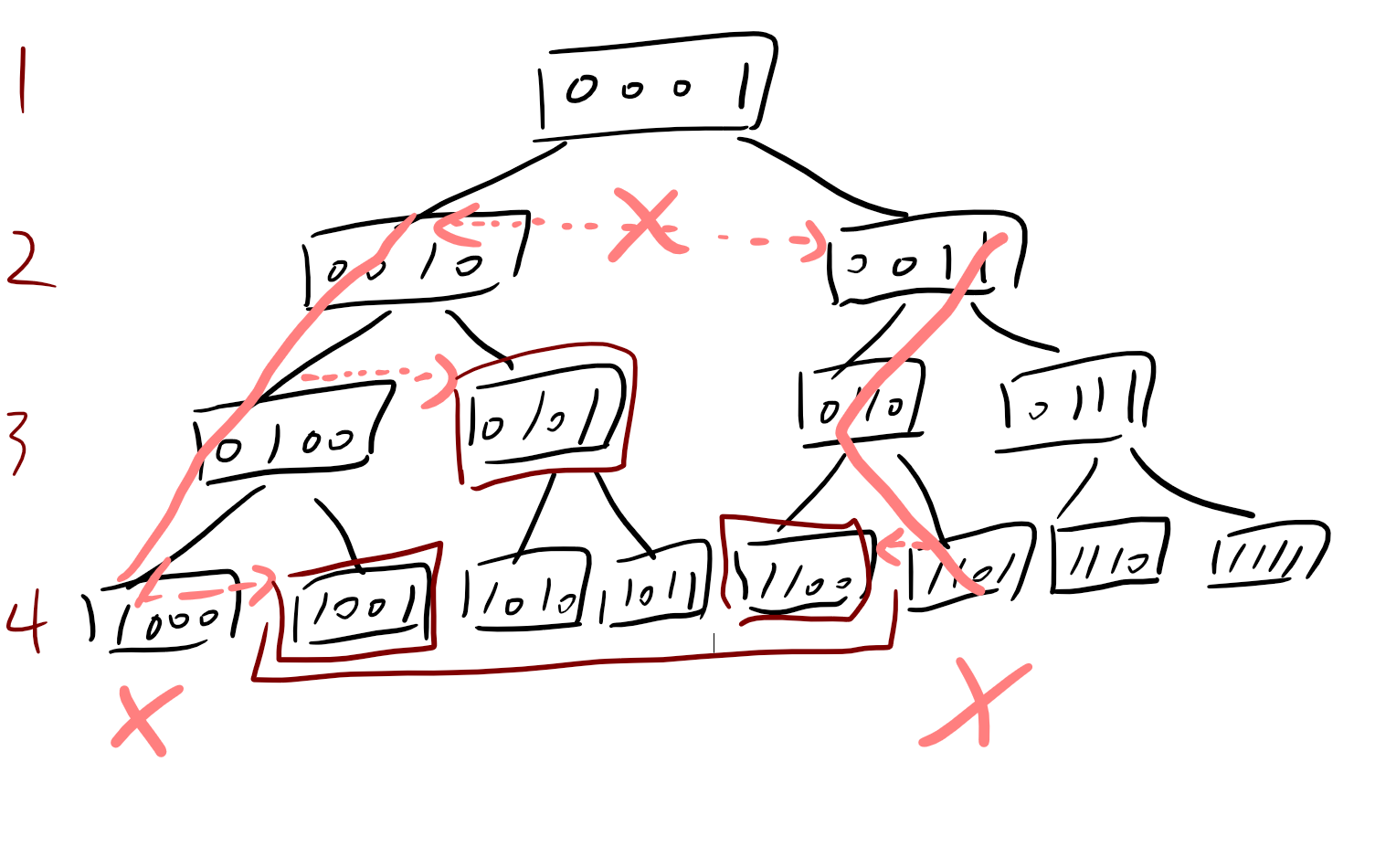

然后两个点一起往上跳父亲。如果左边点的右兄弟正好是右边那个点就停止更新。

中途更新的话就是：
更新左边点的右兄弟（如果有） 和 右边点的左兄弟（如果有）。

被更新的点在图中被框出。

auto modify = [&](tp l, tp r, tp d) -> void {
  tp c = 1, lsum = 0, rsum = 0;
  l += P - 1; r += P + 1;
  for (;;) {
    a[l] += lsum * d; a[r] += rsum * d;
    if ((l ^ r) == 1) break;
    if (~l & 1) { a[l ^ 1] += d * c; t[l ^ 1] += d; lsum += c; }
    if (r & 1) { a[r ^ 1] += d * c; t[r ^ 1] += d; rsum += c; }
    l /= 2; r /= 2; c *= 2;
  }
  while (l /= 2) a[l] += (lsum + rsum) * d;  // 到这里时 l 和 r 已经变成同一个点了。
};

好像我的实现方式不怎么好，写这么长。

懒标记

只需要先跑一遍修改，把途经的节点的标记下传，再进行修改和标记即可。

性能测试

洛谷 P3372

普通的普通线段树 O2：195 ms
标记永久化的普通线段树 O2：165 ms
ZKW 线段树 O2：110 ms

不开 O2 之后 ZKW 的优势更显著。

ZKW 测试代码：

void STRUGGLING([[maybe_unused]] unsigned TEST_NUMBER) {
  tp n, m, P; bin >> n >> m;
  for (P = 1; P + 1 <= n; P *= 2);
  vector<tp> a(P << 1), t(P << 1);
  --P;
  for (tp i = 1; i <= n; ++i) bin >> a[i + P];
  for (tp i = P; i; --i) a[i] = a[i << 1] + a[i << 1 | 1];
  auto query = [&](tp l, tp r) -> tp {
    tp tar = 0, c = 1, lsum = 0, rsum = 0;
    l += P - 1; r += P + 1;
    for (;;) {
      tar += lsum * t[l] + rsum * t[r];
      if ((l ^ r) == 1) break;
      if (~l & 1) { tar += a[l ^ 1]; lsum += c; }
      if (r & 1) { tar += a[r ^ 1]; rsum += c; }
      l /= 2; r /= 2; c *= 2;
    }
    while (l /= 2) tar += (lsum + rsum) * t[l];
    return tar;
  };
  auto modify = [&](tp l, tp r, tp d) -> void {
    tp c = 1, lsum = 0, rsum = 0;
    l += P - 1; r += P + 1;
    for (;;) {
      a[l] += lsum * d; a[r] += rsum * d;
      if ((l ^ r) == 1) break;
      if (~l & 1) { a[l ^ 1] += d * c; t[l ^ 1] += d; lsum += c; }
      if (r & 1) { a[r ^ 1] += d * c; t[r ^ 1] += d; rsum += c; }
      l /= 2; r /= 2; c *= 2;
    }
    while (l /= 2) a[l] += (lsum + rsum) * d;
  };
  while (m--) {
    tp op, x, y; bin >> op >> x >> y;
    if (op == 1) {
      tp k; bin >> k;
      modify(x, y, k);
    } else bin << query(x, y) << '\n';
  }
}

---

• 分类： 学习笔记
• 最后更新于：2024-02-01 10:50:27^UTC+8
• 标签： 无标签