强连通缩点 学习笔记

题意

强连通缩点 算法

Kosaraju 算法

首先，我们对图进行 DFS，按 DFS 中返回的顺序编号，如图

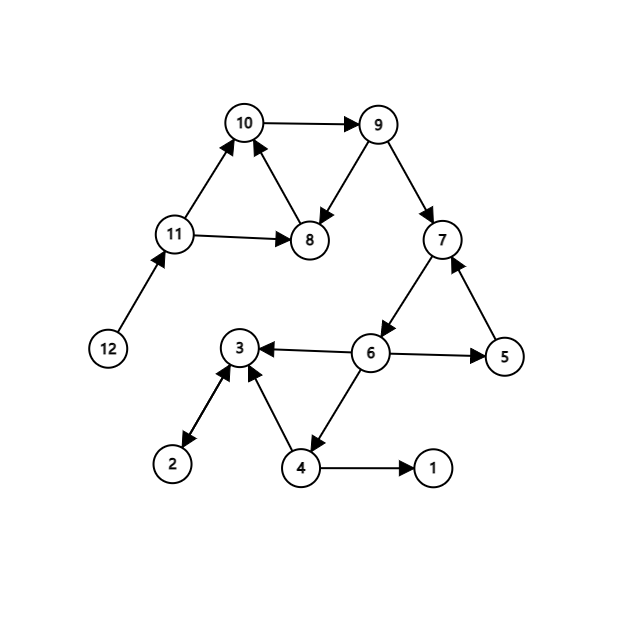
然后，我们将所有的边 反向，如图

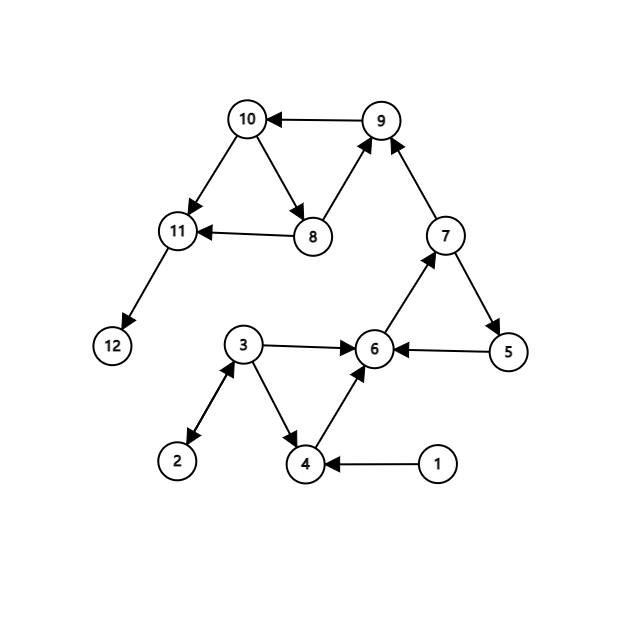
接下来，按顶点编号 从大到小，再进行搜索，搜到的连通块，就是 一个强连通分量。

比如，在搜索编号为 $10$ 的顶点时，搜到了 $8\ 9\ 10$，所以 $8, 9, 10$ 这三个点是 一个强连通分量。

搜完之后的结果：

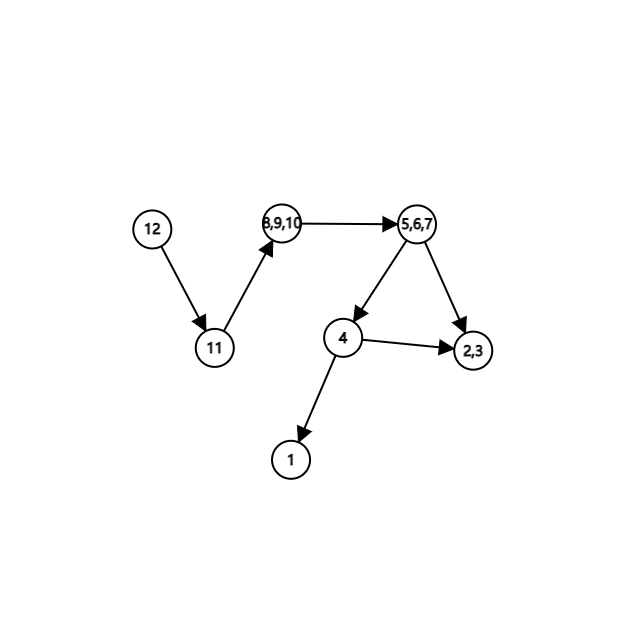
正确性

在 Kosaraju 算法中，先将有向图 $G$ 的边反向得到 $G'$，然后计算 $G'$ 的拓扑序 $ord$，然后再将 $G$ 按照 $ord$ 的顺序进行 DFS。

1. 对 $G$ 进行 DFS，出现从 $x$ 递归到 $y$ 的情况，说明在 $G$ 中存在一条有向边 $x \to y$。
2. 在 $ord$ 中，只有 $x$ 在 $y$ 前面的情况下，才可能出现从 $x$ 递归到 $y$ 的情况。
3. 如果存在 $x \to y$，那么在 $ord$ 中，$y$ 一定在 $x$ 前面。
4. 如果拓扑序是 $x$ 在 $y$ 前面，又存在 $y \to x$，那么 $x \to y$ 也成立。即 $x$ 和 $y$ 在一个强连通分量中。

代码

// By rbtree (https://rbtr.ee) :\
// Please submit with C++14!
#include <algorithm>
#include <array>
#include <cmath>
#include <functional>
#include <iostream>
#include <list>
#include <map>
#include <numeric>
#include <queue>
#include <random>
#include <set>
#include <tuple>
#include <unordered_map>
#include <utility>
#include <valarray>
#include <vector>
#define ra _Read_Int()
#define rc _Read_Char()
#define rs _Read_String()
#define rr _READ_RAW_::_Rd()
#define iotop _Get_IO_Top()
#define __FAST__ 1
#ifdef ___RB_DEBUG___
#include "rb_debug.h"
#else
#define dbg(...)
#define dputs(...)
#endif

using tp = long long;
tp _Read_Int();
char _Read_Char();
char _Get_IO_Top();
std::string _Read_String();
namespace _READ_RAW_ {
char _Rd();
}  // namespace _READ_RAW_
using namespace std;
constexpr bool __MTCS__ = 0;
constexpr tp _BUF_SIZE_ = 217'217'21;

////////////////////////////////////////////////////////////////////////////////
////////////////////////////////////////////////////////////////////////////////

namespace __SOL__ {
constexpr tp Hat_N = 10003, Hat_M = 1e5 + 3;

bool vis[Hat_N];
tp w[Hat_N], sccno[Hat_N], f[Hat_N], sccw[Hat_N], u[Hat_M], v[Hat_M];
list<tp> stk, g[Hat_N], fg[Hat_N];
tp n, cnt;

void dfs(tp x) {
  if (vis[x]) {
    return;
  }
  vis[x] = 1;
  for (auto&& i : g[x]) {
    dfs(i);
  }
  stk.push_back(x);
}

void mark(tp x, tp f) {
  sccno[x] = f;
  sccw[f] += w[x];
  for (auto&& i : fg[x]) {
    if (!sccno[i]) {
      mark(i, f);
    }
  }
}

void kosaraju() {
  for (tp i = 1; i <= n; ++i) {
    dfs(i);
  }
  while (stk.size()) {
    if (!sccno[stk.back()]) {
      mark(stk.back(), ++cnt);
    }
    stk.pop_back();
  }
}

void dp(tp x) {
  if (f[x]) {
    return;
  }
  for (auto&& i : g[x]) {
    dp(i);
    f[x] = max(f[x], f[i]);
  }
  f[x] += sccw[x];
}

void main([[maybe_unused]] size_t __CASE__) {  // :/
  n = ra;
  tp m = ra, tar = 0;
  for (tp i = 1; i <= n; ++i) {
    w[i] = ra;
  }
  for (tp i = 0; i < m; ++i) {
    u[i] = ra;
    v[i] = ra;
    g[u[i]].push_back(v[i]);
    fg[v[i]].push_back(u[i]);
  }
  kosaraju();
  for (tp i = 1; i <= n; ++i) {
    g[i].clear();
  }
  for (tp i = 0; i < m; ++i) {
    if (sccno[u[i]] != sccno[v[i]]) {
      g[sccno[u[i]]].push_back(sccno[v[i]]);
    }
  }
  for (tp i = 1; i <= cnt; ++i) {
    dp(i);
    tar = max(tar, f[i]);
  }
  printf("%lld\n", tar);
}  // :)
}  // namespace __SOL__

////////////////////////////////////////////////////////////////////////////////
////////////////////////////////////////////////////////////////////////////////

signed main() {
  tp __MTCS__ = ::__MTCS__ ? ra : 1;
  for (tp __i = 1; __i <= __MTCS__; ++__i) {
    __SOL__::main(__i);
  }
  return EXIT_SUCCESS;
}

namespace _READ_RAW_ {
#if __FAST__
std::array<char, _BUF_SIZE_ + 1> _BUF_;
std::array<char, _BUF_SIZE_>::iterator __Cur = _BUF_.begin(), __End = __Cur + 1;

char _Rd() {
  if (++__Cur == __End) {
    __Cur = _BUF_.begin();
    __End = __Cur + fread(_BUF_.begin(), 1, _BUF_SIZE_, stdin);
    *__End++ = 10;
  }
  return *__Cur;
}
}  // namespace _READ_RAW_

char _Get_IO_Top() {
  if (_READ_RAW_::__Cur + 1 == _READ_RAW_::__End) {
    _READ_RAW_::__Cur = _READ_RAW_::_BUF_.begin();
    _READ_RAW_::__End = _READ_RAW_::__Cur +
                        fread(_READ_RAW_::_BUF_.begin(), 1, _BUF_SIZE_, stdin);
    if (_READ_RAW_::__Cur == _READ_RAW_::__End) {
      return --_READ_RAW_::__Cur, -1;
    } else {
      return *_READ_RAW_::__Cur--;
    }
  }
  return *(_READ_RAW_::__Cur + 1);
#else
char _Rd() {
  return getchar();
}
#endif
}  // namespace _READ_RAW_

tp _Read_Int() {
  bool __neg(0);
  char __c(_READ_RAW_::_Rd());
  tp __val;
  for (; __c < 48 || __c > 57; __c = _READ_RAW_::_Rd()) {
    __neg = __c == 45;
  }
  __val = __c & 15;
  for (__c = _READ_RAW_::_Rd(); __c > 47 && __c < 58; __c = _READ_RAW_::_Rd()) {
    __val = __val * 10 + (__c & 15);
  }
  return __neg ? ~__val + 1 : __val;
}
char _Read_Char() {
  char __c(_READ_RAW_::_Rd());
  for (; __c == 32 || __c == 10 || __c == 13; __c = _READ_RAW_::_Rd()) {
  }
  return __c;
}
std::string _Read_String() {
  char __c(_READ_RAW_::_Rd());
  std::string __val;
  for (; __c == 32 || __c == 10 || __c == 13; __c = _READ_RAW_::_Rd()) {
  }
  do {
    __val.push_back(__c);
    __c = _READ_RAW_::_Rd();
  } while (__c != 32 && __c != 10 && __c != 13);
  return __val;
}

//\
 ___       ___         ___________     \
|\  \     |\  \       |\    ___   \
\ \  \    \ \  \      \ \   \|_\   \
 \ \  \  __\ \  \      \ \    ___   \
  \ \  \|\__\_\  \      \ \   \  \   \
   \ \____________\      \ \___\  \___\
    \|____________|       \|___|  |___|

/*#################################################################
#.................................................................#
#............................This.Code.Was.Created.By.RBTree......#
#.............#......#...............Limiting-Factor..............#
#............#.#....#.#.................Soul-Code.................#
#.............########............................................#
#............#........#..##############################...........#
#...........#..V....V......#..#........................#..#...#...#
#............#........#....#..........###..###..........#..#.#.#..#
#............#..X##X..#..#............#....#.#...........#..#...#.#
#...........#...N##N...#..#...........###..###..........#.........#
#.......MOE..#..@.....#....#.#.#.#...................#.#..........#
#.............########.....#.#.#.##############.#.#..#.#..........#
#..........................#.#.#.#.............#.#.#.#.#..........#
#......#########...........#.#.#.#.................#.#.#..........#
#.....#.........#..........#.#.#.#.................#.#.#..........#
#.#.#.#G#R#A#S#S#.#.#......#.#.#.#.................#.#.#..........#
#.###################......#.#.#.#.................#.#.#..........#
#...........................#.#.#...................#.#...........#
#.................................................................#
#################################################################*/

---

Tarjan 算法

以后有空写

---

• 分类： 学习笔记
• 最后更新于：2024-06-30 01:48:33^UTC+8
• 标签： 缩点