概述
多项式插值算法用于寻找一个恰好通过给定数据点的多项式。
问题形式
给定 $k + 1$ 个互异数据点 $\left(x_i, y_i\right)$,找到一个 $n$ 次多项式 $f\left(x\right)$,使得对于任意的 $0 \leq i \leq k$,有 $f\left(x_i\right) = y_i$。在某些情况下,我们只需求出 $f\left(a\right)$ 的值,而不需要求出 $f\left(x\right)$ 的每个系数。
拉格朗日(Lagrange)插值法
定义 拉格朗日基本多项式(Lagrange basis polynomial) 为:
$$\ell_j\left(x\right) = \prod\limits_{0 \leq m \leq k, m \neq j} \frac{x - x_m}{x_j - x_m}$$
如果使用 克罗内克(Kronecker) $\delta$ 函数 进行描述:$\ell_j\left(x_m\right) = \delta_{jm}$
拉格朗日插值公式是如下的线性组合:
$$L\left(x\right) = \sum\limits_{j = 0}^ky_j\ell_j\left(x\right)$$
由于每个 拉格朗日基本多项式 的次数都不超过 $k$,所以 $L\left(x\right)$ 的次数也不超过 $k$。
而对于每个 $m$:$L\left(x_m\right) = \sum\limits_{j = 0}^ky_j\delta_{mj} = y_m$
同时,插值多项式是唯一的:
假设有一个 $k$ 次多项式 $M\left(x\right)$ 是插值的答案。那么 $M\left(x\right) - L\left(x\right)$ 在 $k + 1$ 个不同点 $\left\{x_0, x_1, \ldots, x_k\right\}$ 上都是 $0$,但是当一个 $k$ 次多项式具有 $k + 1$ 个零点时,可以确定,该多项式的值恒等于 $0$。因此:$M\left(x\right) - L\left(x\right) = 0$ 或者说 $M\left(x\right) = L\left(x\right)$。
原理
这里给出我的理解方式。
假设现在有三个目标点
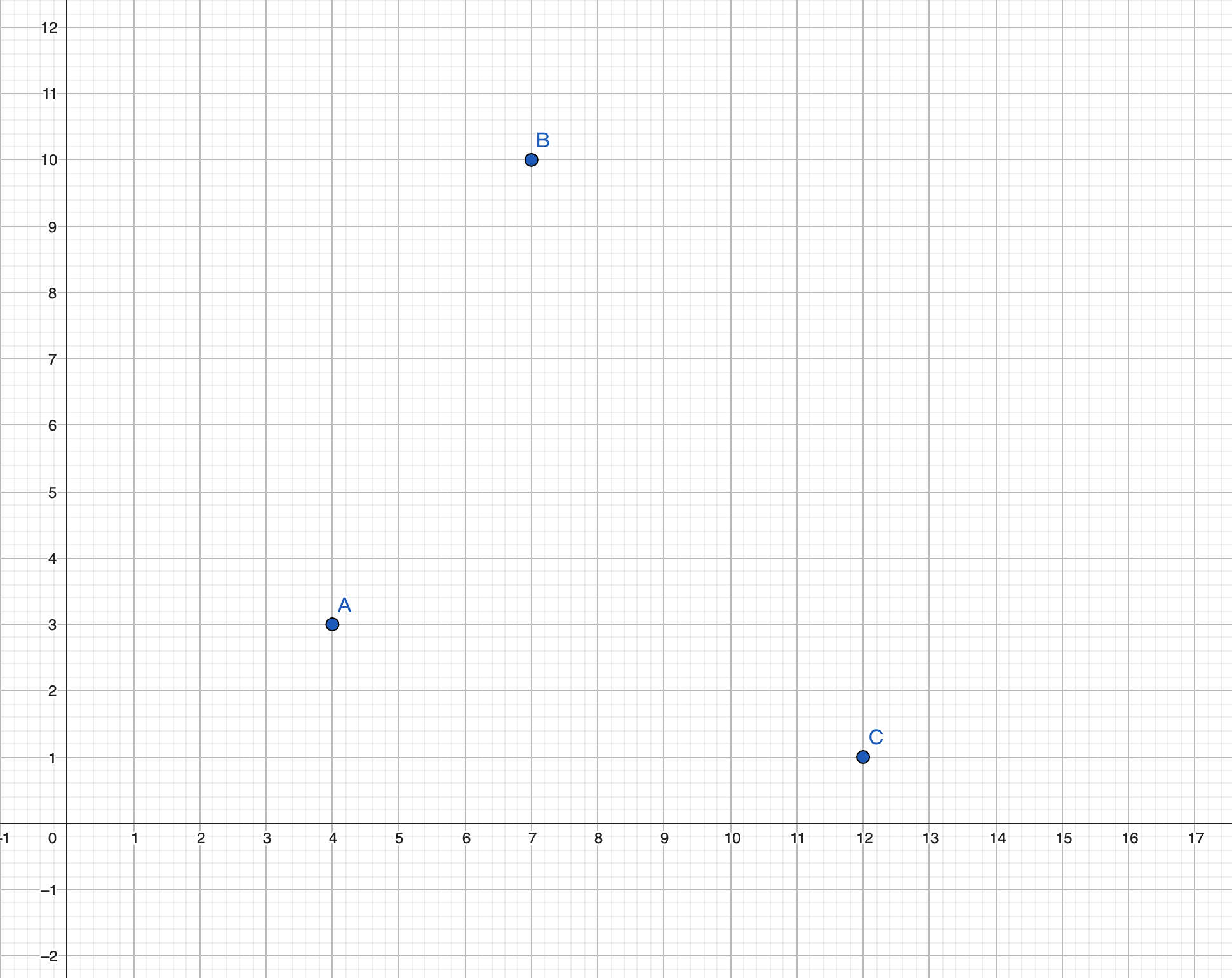
我们构造三个函数:
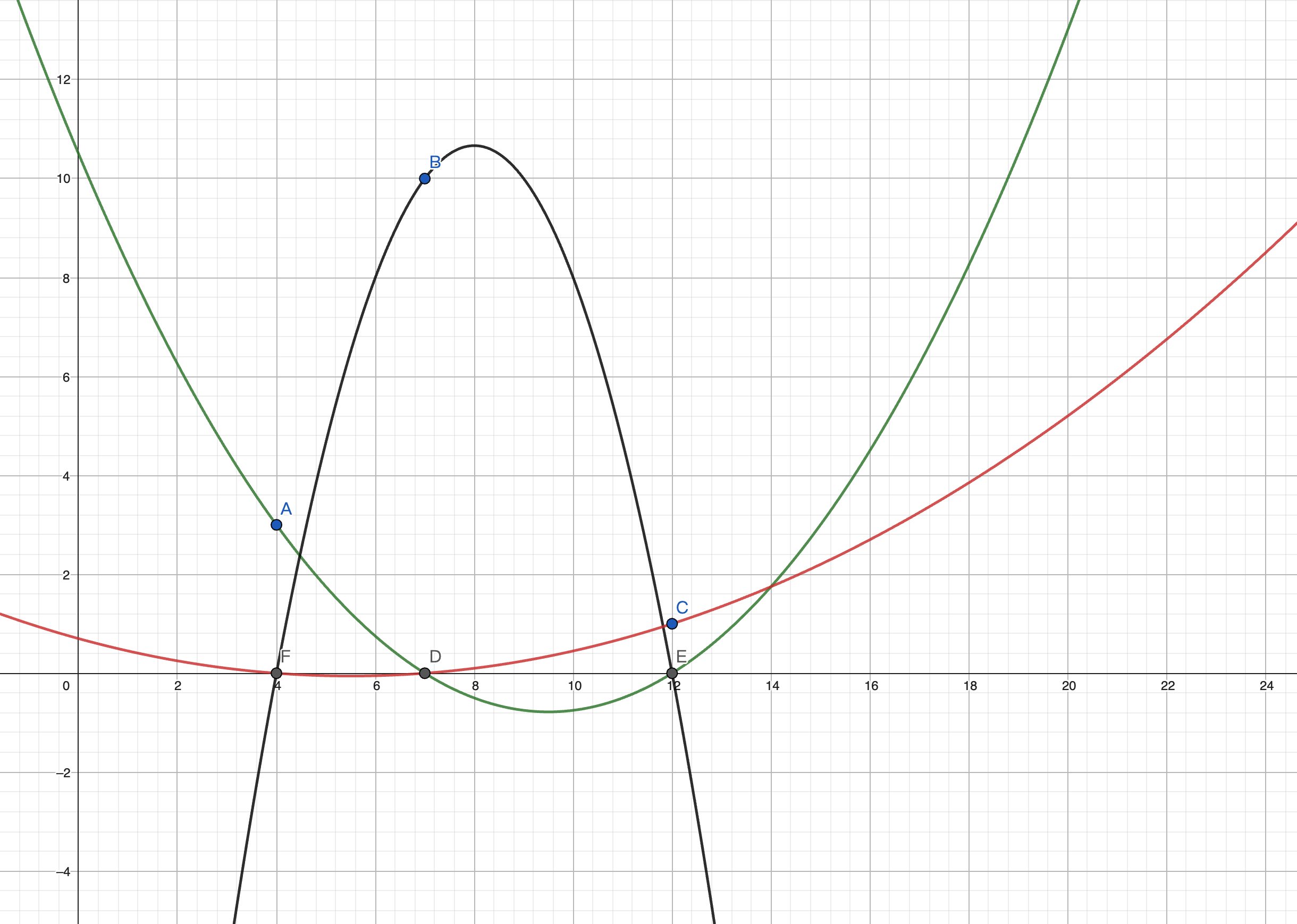
注意看,每个函数都恰好经过一个不同的目标点 和 两个零点,这些零点的 $x$ 坐标均与一个目标点相同。
例如这根红线,经过的 $F$ 点的 $x$ 坐标与目标点 $A$ 的横坐标都是 $4$;经过的 $D$ 点的 $x$ 坐标与目标点 $B$ 的横坐标都是 $7$;而又经过了目标点 $C$。
这样,当我们把这三个函数相加:
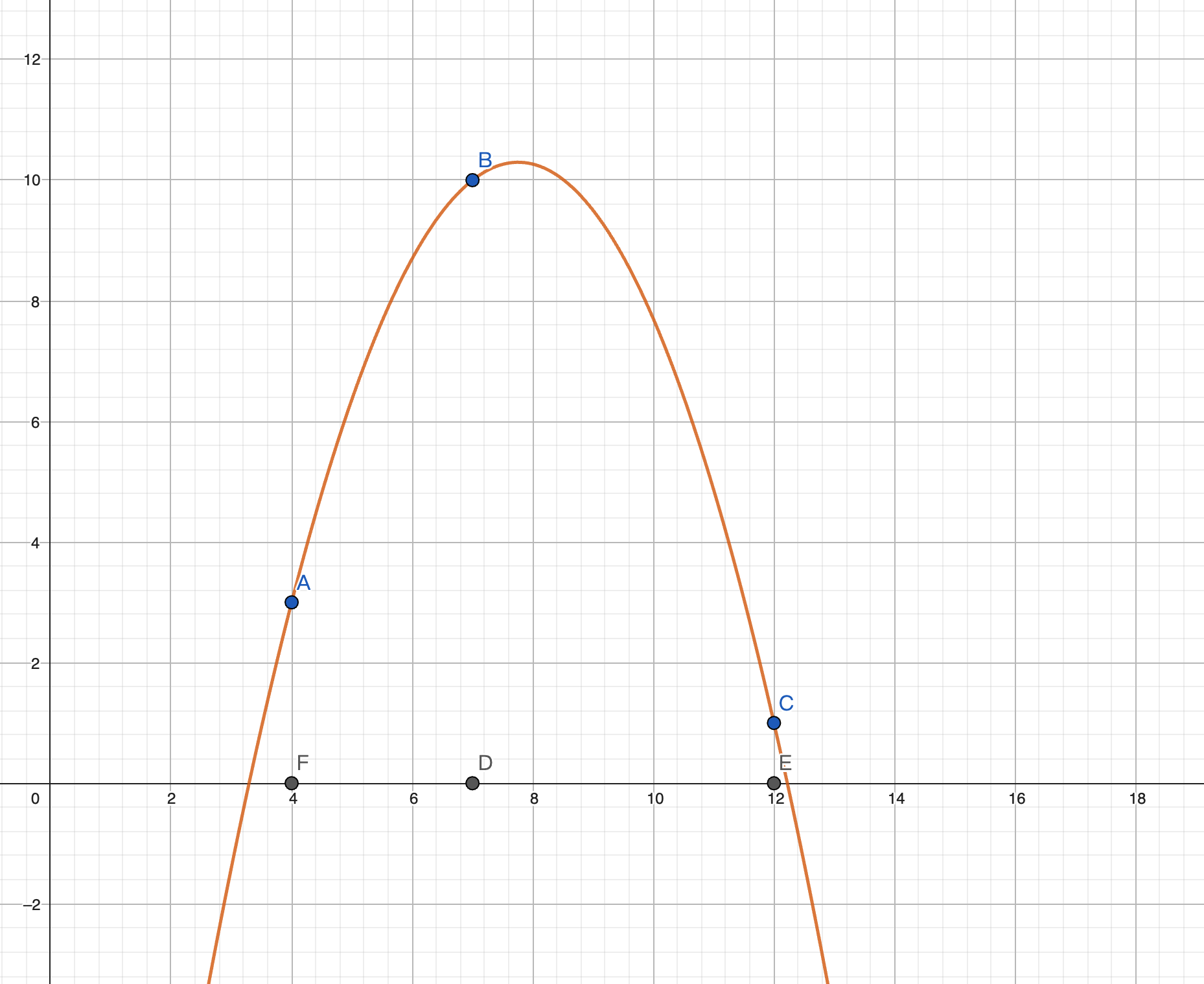
每个目标点就刚好被穿过。
此时再观察拉格朗日基本多项式:
$$\ell_j\left(x\right) = \prod\limits_{0 \leq m \leq k, m \neq j} \frac{x - x_m}{x_j - x_m}$$
只有 $\ell_j\left(x_j\right) = 1$,其它 $\ell_j\left(x_i\right)$ 的值都为 $0$。
而最后拉格朗日插值公式:
$$L\left(x\right) = \sum\limits_{j = 0}^ky_j\ell_j\left(x\right)$$
又 给它乘上了一个 $y_j$,这就是的该函数刚好经过一个目标点。
重心拉格朗日插值法(Barycentric form)
如果需要动态加入点,那么普通的拉格朗日插值就需要整个重新计算一遍。重心拉格朗日插值法只需要线性时间即可完成动态点加入。
我们再来看看拉格朗日插值公式
$$ \begin{aligned} L\left(x\right) &= \sum\limits_{j = 0}^ky_j\prod\limits_{0 \leq m \leq k, m \neq j}\frac{x - x_m}{x_j - x_m} \\ &= \left(\prod\limits_{j = 0}^k\left(x - x_j\right)\right)\sum\limits_{j = 0}^k\frac1{x - x_j} \cdot \left(\prod\limits_{0 \leq m \leq k, m \neq j}\frac{y_j}{x_j - x_m}\right) \end{aligned} $$
因此,每次加入一个新点,我们值需要计算 $\prod\limits_{0 \leq m \leq k, m \neq j}\frac{y_j}{x_j - x_m}$ 即可。
牛顿(Newton)插值法
牛顿插值法也只需要线性时间即可完成动态点加入。
定义 牛顿基本多项式(Newton basis polynomials) 为:
$$n_j\left(x\right) = \prod\limits_{i = 0}^{j - 1}\left(x - x_i\right)$$
牛顿插值公式是如下的线性组合:
$$N\left(x\right) = \sum\limits_{j = 0}^ka_jn_j\left(x\right)$$
其中,$a_n = \left[y_0, y_1, \ldots, y_n\right]$,而 $\left[y_0, y_1, \ldots, y_n\right]$ 表示 差商(Divided differences)。
差商
$$ \begin{aligned} \left[y_0\right] &= y_0 \\ \left[y_0, y_1\right] &= \frac{\left[y_1\right] - \left[y_0\right]}{x_1 - x_0} \\ \left[y_0, y_1, y_2\right] &= \frac{\left[y_1, y_2\right] - \left[y_0, y_1\right]}{x_2 - x_0} \\ \left[y_0, y_1, y_2, y_3\right] &= \frac{\left[y_1, y_2, y_3\right] - \left[y_0, y_1, y_2\right]}{x_3 - x_0} \\ \left[y_0, \ldots, y_k\right] &= \frac{\left[y_1, \ldots, y_k\right] - \left[y_0, \ldots, y_{k - 1}\right]}{x_k - x_0} \end{aligned} $$
注意到 $k$ 阶差商就是 两个 $k - 1$ 阶差商 的差商。
原理
假设现在只有两个点 $\left(x_0, y_0\right)$ 和 $\left(x_1, y_1\right)$。求经过这两个点的函数 $g\left(x\right)$。
设 $g\left(x\right) = y_0 + c_1 \left(x - x_0\right)$,代入 $g\left(x_1\right) = y_1$ 即可解出 $c_1$。
我们让 $c_1$ 乘上 $\left(x - x_0\right)$ 的原因是保证 $g\left(x_0\right) = y_0$。
假设现在有三个点 $\left(x_0, y_0\right), \left(x_1, y_1\right)$ 和 $\left(x_2, y_2\right)$。求经过这两个点的函数 $h\left(x\right)$。
设 $h\left(x\right) = g\left(x\right) + c_2 \left(x - x_0\right)\left(x - x_1\right)$,代入 $h\left(x_2\right) = y_2$ 即可解出 $c_2$。
此时再观察牛顿多项式:
$$N\left(x\right) = \left[y_0\right] + \left[y_0, y_1\right]\left(x - x_0\right) + \cdots + \left[y_0, \ldots, y_k\right]\left(x - x_0\right)\left(x - x_1\right) \cdots \left(x - x_{k - 1}\right)$$
其实 $c_i$ 的解就是对应的差商。
代码
网上找了一圈没看见一个写牛顿插值动态插入的,只好自己写一个了。
代码大家应该都看得懂的。
dvdiff 表示差商,X 是 $x_i$,n 表示 $\prod\limits_{i = 0}^k\left(x - x_i\right)$,N 表示插出来的各项系数,从高到低的。
大家可以当个模板使用,注意使用前先 setmod 一下。当然有需要的话可以把这个改成实数域的,也很好改。
class Newton_Poly_Int_Builder {
vector<vector<tp>> dvdiff; // dvdiff[a][b] -> [a, a + 1, ..., a + b];
vector<tp> X, n, N;
tp mod;
public:
void clear() {
X.clear();
dvdiff.clear();
n.clear();
N.clear();
}
void setmod(tp x) {
mod = x;
clear();
}
tp positive(tp x) {
if (x < 0) return x + mod;
else if (x >= mod) return x - mod;
return x;
}
void insert(tp x, tp y) {
dvdiff.push_back(vector<tp>(1, y));
for (tp i = dvdiff.size() - 2; i >= 0; --i)
dvdiff[i].push_back(positive(dvdiff[i + 1].back() - dvdiff[i].back()) * RCAL::inverse(positive(x - X[i]), mod) % mod);
tp c = dvdiff.front().back();
vector<tp> tmp = n;
if (n.empty()) n = vector<tp>(1, 1);
else {
for (auto& i : tmp) i = positive(-i * X.back() % mod);
n.push_back(0);
for (tp i = 0; i < tmp.size(); ++i) n[i + 1] = (n[i + 1] + tmp[i]) % mod;
}
tmp = n;
for (auto& i : tmp) i = positive(i * c % mod);
N.swap(tmp);
for (tp i = 0; i < tmp.size(); ++i) N[i + 1] = positive(N[i + 1] + tmp[i]);
X.push_back(x);
}
tp query(tp x) {
tp pw = 1, ret = 0;
for (tp i = N.size() - 1; i >= 0; --i) {
ret = (ret + N[i] * pw) % mod;
pw = pw * x % mod;
}
return ret;
}
} Newton_Poly_Int;参考
https://en.wikipedia.org/wiki/Lagrange_polynomial
https://zh.wikipedia.org/wiki/%E6%8B%89%E6%A0%BC%E6%9C%97%E6%97%A5%E6%8F%92%E5%80%BC%E6%B3%95
https://en.wikipedia.org/wiki/Newton_polynomial
https://www.zhihu.com/question/22320408/answer/141973314
https://en.wikipedia.org/wiki/Divided_differences
https://www.zhihu.com/question/58333118