概述
不同方法的收敛速度和迭代次数不同,我们会根据需要找到最适合的方法。
下文计划描述的算法有 GD,SGD,PAGE。
$\epsilon$-solution
我们需要找到一个方式来描述算法当前解的优劣。
最简单的方法就是用 $\left\Vert\nabla f\left(\hat x\right)\right\Vert_2$。
那我们称一个解是一个 $\epsilon$-solution,仅当$\left\Vert\nabla f\left(\hat x\right)\right\Vert_2 \leq \epsilon$。
GD
GD(梯度下降)有关的内容可以在 这里 找到。
结论:GD 的收敛速度为 $\mathcal O\left(\frac n{\epsilon^2}\right)$,具体来说,GD 需要 $\mathcal O\left(\frac1{\epsilon^2}\right)$ 次迭代,每次迭代需要计算 $n$ 个梯度。
推导
可以跳过。
回顾 GD 的定义式:$x^{t + 1} \leftarrow x^t - \eta\nabla f\left(x^t\right)$
回顾 $L$-smooth 的定义式:$f\left(y\right) \leq f\left(x\right) + \left\langle\nabla f\left(x\right), y - x\right\rangle + \frac L2\left\Vert y - x\right\Vert^2$
$$ \begin{aligned} f\left(x^{t + 1}\right) &\leq f\left(x^t\right) + \left\langle \nabla f\left(x^t\right), x^{t + 1} - x^t\right\rangle + \frac L2\left\Vert x^{t + 1} - x^t\right\Vert^2\\ &= f\left(x^t\right) - \eta\left\langle\nabla f\left(x^t\right), \nabla f\left(x^t\right)\right\rangle + \frac{L\eta^2}2\left\Vert \nabla f\left(x^t\right)\right\Vert^2\\ &\leq f\left(x^t\right) - \frac\eta2\left\Vert\nabla f\left(x^t\right)\right\Vert^2 \end{aligned} $$
其中 $\eta \leq \frac1L$。
$$\frac\eta2\sum\limits_{0 \leq t < T}\left\Vert\nabla f\left(x^t\right)\right\Vert^2 \leq \sum\limits_{0 \leq t < T}\left(f\left(x^{t + 1}\right) - f\left(x^t\right)\right) \leq \Delta_0 \overset{\mathsf{def}}{=}f\left(x^0\right) - f^*$$
令 $\eta = \frac1L$,并从 $\left\{x^t\right\}_{0 \leq t < T}$ 中随机选择一个 $\epsilon$-solution:
$$\mathbb E\left[\left\Vert\nabla f\left(\hat x_T\right)\right\Vert^2\right] \leq \frac{2\Delta_0L}T = \epsilon^2$$
迭代次数 $T = \mathcal O\left(\frac1{\epsilon^2}\right)$。
注意 $\mathbb E\left[\left\Vert\nabla f\left(\hat x_T\right)\right\Vert\right] \leq \sqrt{\mathbb E\left[\left\Vert\nabla f\left(\hat x_T\right)\right\Vert^2\right]} \leq \epsilon$。
SGD
若要求 $\mathbb E_i\left[\left\Vert\nabla f_i\left(x\right) - \nabla f\left(x\right)\right\Vert^2\right] \leq \sigma^2$
结论:SGD 的收敛速度为 $\mathcal O\left(\frac1{\epsilon^2} + \frac{\sigma^2}{\epsilon^4}\right)$,具体来说,SGD 需要 $\mathcal O\left(\frac{\sigma^2}{\epsilon^4}\right)$ 次迭代,每次迭代计算 $1$ 个梯度。
推导
懒得写了,以后再说(
PAGE
此处就有两个问题:
- 我们能否取消有界梯度差?
- 我们能否同时继承 GD 和 SGD 的优点,即在不增加迭代次数的情况下降低每次迭代的梯度计算开销?
隆重介绍 PAGE 算法(ProbAbilistic Gradient Estimator),同时解决上述两个问题。
PAGE 更新(Li et al., ICML'21)
$$ \boxed { \begin{array}{l} 1) \; x^{t + 1} \leftarrow x^t - \eta g^t \\ 2) \; g^{t + 1} \leftarrow \begin{cases} \frac1b\sum\limits_{i \in I}\nabla f_i\left(x^t\right) & \text{w.p.} \; p_t \\ g^t + \frac1{b'}\sum\limits_{i \in I'}\left(\nabla f_i\left(x^{t + 1}\right) - \nabla f_i\left(x^t\right)\right) & \text{w.p.} \; 1 - p_t \end{cases} \\ 3) \; \text{repeat 1) and 2)} \end{array} } $$
其中 $I, I' \in \left[n\right]$,表示随机小批量数据样本,且有 $\left\lvert I\right\rvert = b$ 和 $\left\lvert I'\right\rvert = b'$
PAGE 以 $p_t$ 的概率使用小批量(minibatch)SGD 更新,和以 $1 - p_t$ 的概率重新使用上一个梯度 $g^t$,并附带一个 小调整(如果 $b' \ll b$,计算开销更小)
回到我们的问题:我们能否取消有界梯度差?
引理 1(variance reduction)
在 $L$-smooth 的前提下:
$$\boxed{\mathbb E_t\left[\left\Vert g^{t + 1} - \nabla f\left(x^{t + 1}\right)\right\Vert^2\right] \leq \left(1 - p_t\right) \left\Vert g^t - \nabla f\left(x^t\right)\right\Vert^2 + \frac{\left(1 - p_t\right)L^2}{b'}\left\Vert x^{t + 1} - x^t\right\Vert^2}$$
然后,回到第二个问题:我们能否同时继承 GD 和 SGD 的优点?
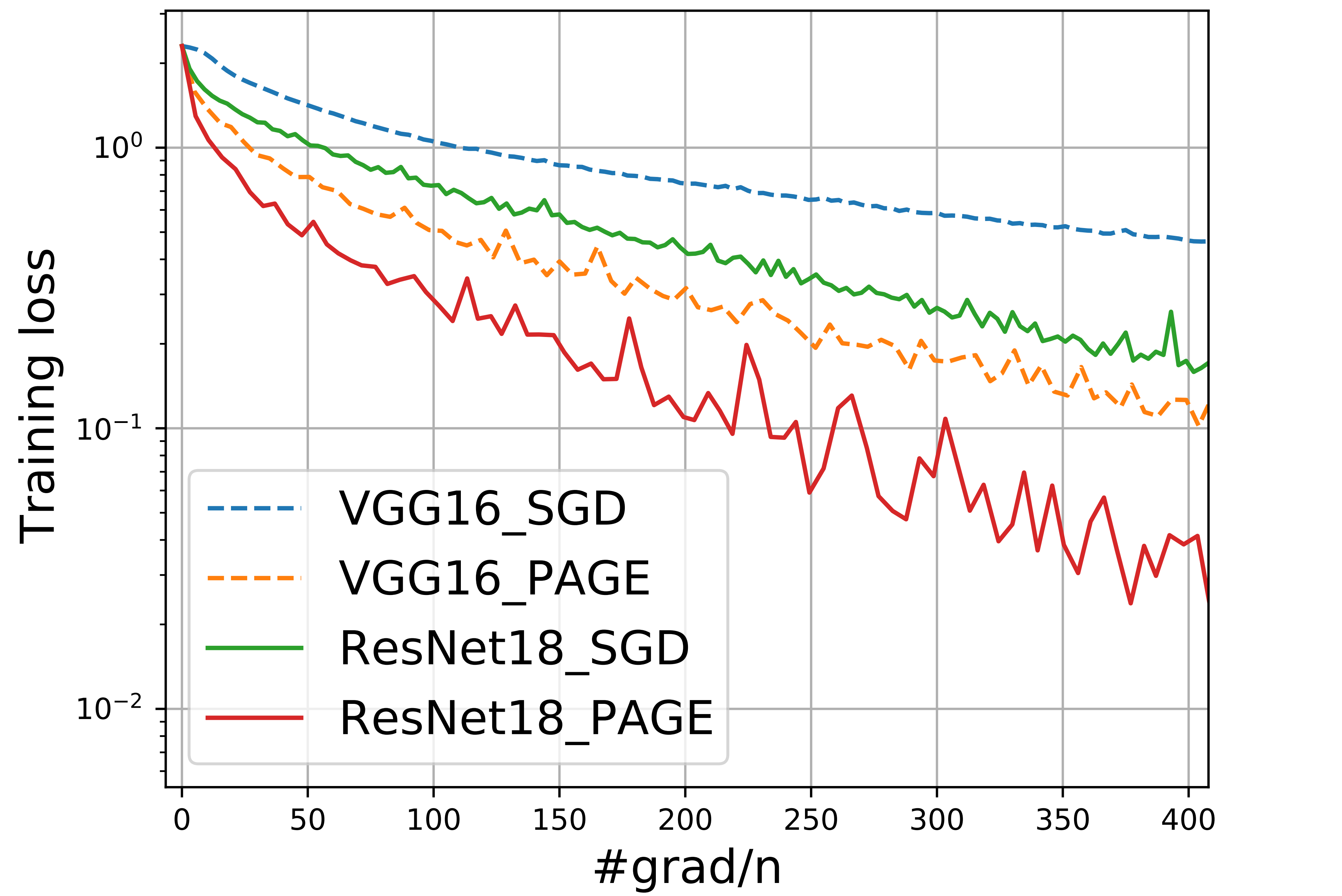
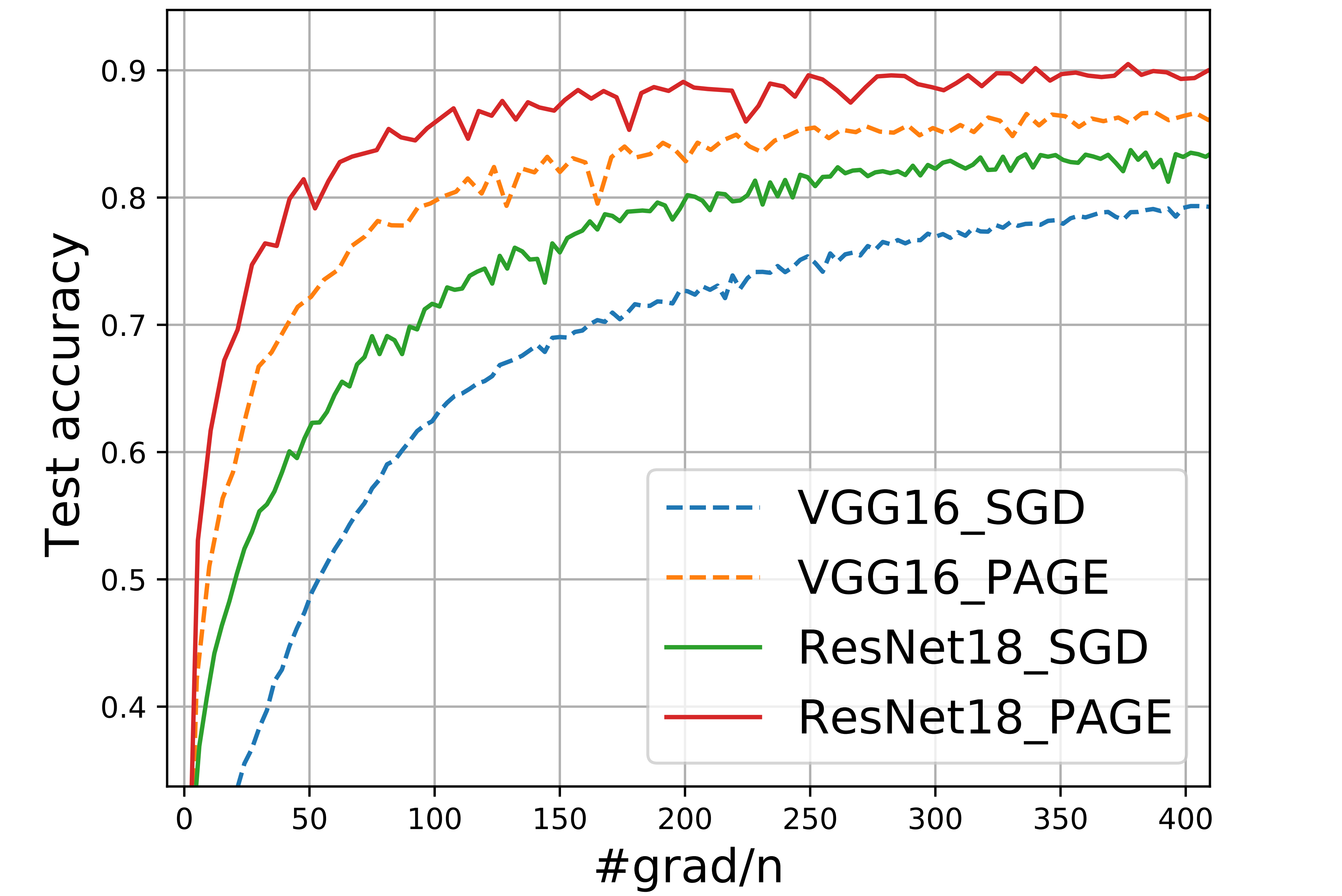
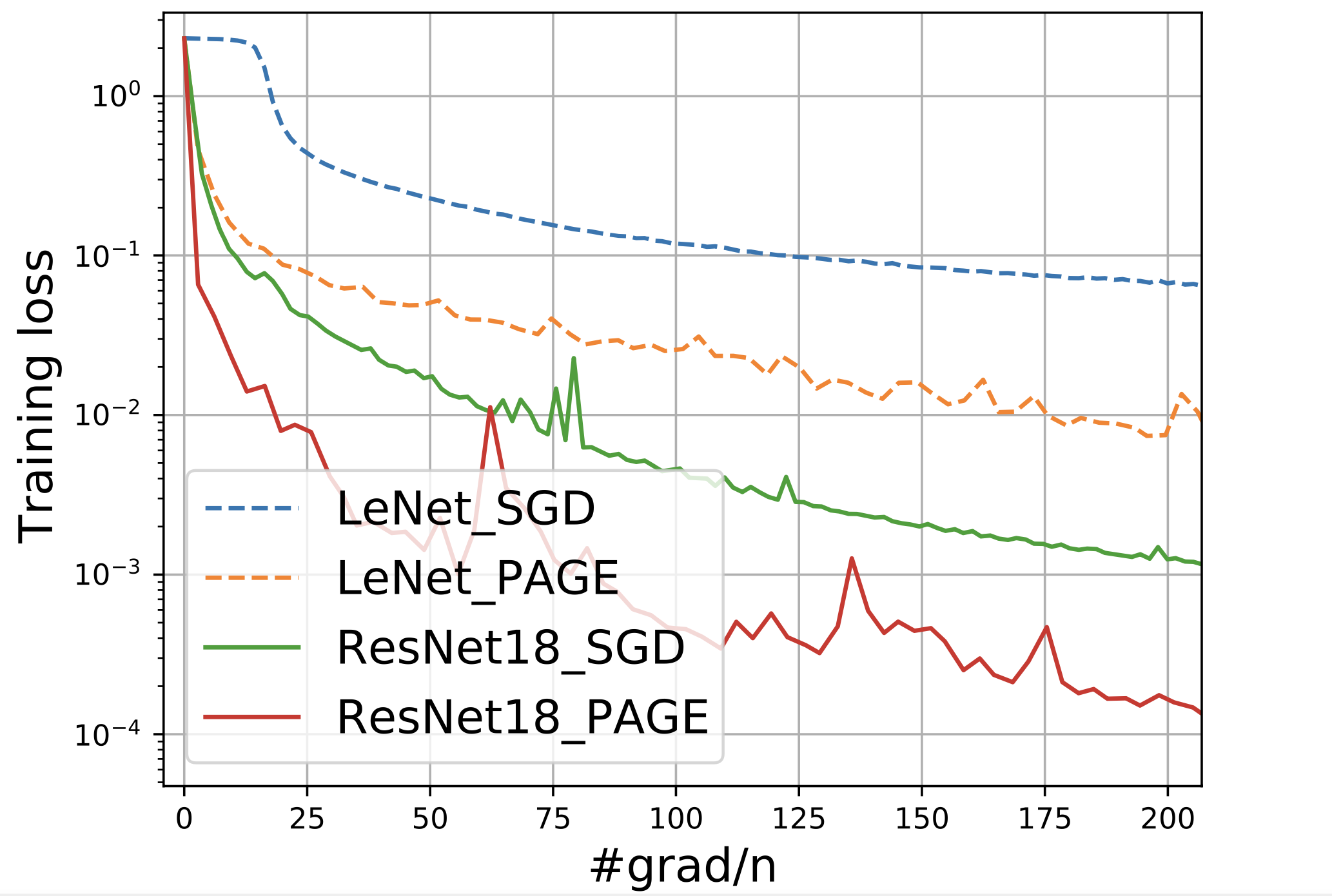
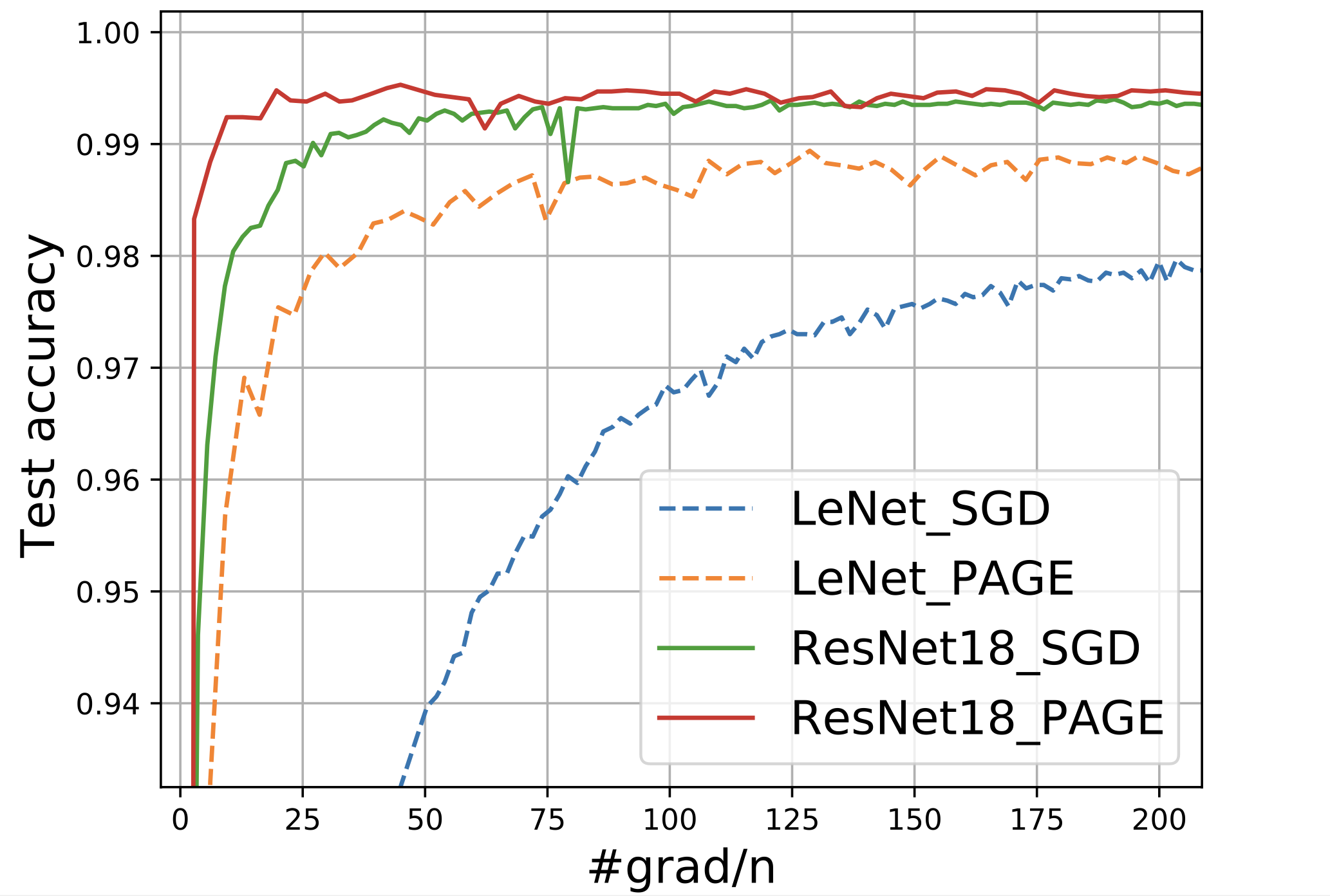
结论是:PAGE 的收敛速度为 $\mathcal O\left(n + \frac{\sqrt n}{\epsilon^2}\right)$。
推导
引理 2(descent lemma)
$$\boxed{f\left(x^{t + 1}\right) \leq f\left(x^t\right) - \frac\eta2\left\Vert\nabla f\left(x^t\right)\right\Vert^2 - \left(\frac1{2\eta} - \frac L2\right)\left\Vert x^{t + 1} - x^t\right\Vert^2 + \frac\eta2\left\Vert g^t - \nabla f\left(x^t\right)\right\Vert^2}$$
令 $\Phi_t \overset{\mathsf{def}}{=} f\left(x^t\right) - f^* + \frac\eta{2p}\left\Vert g^t - \nabla f\left(x^t\right)\right\Vert^2$,如果 $\eta \leq \frac1{L\left(1 + \sqrt b/b'\right)}$ 且 $p_t \equiv \frac{b'}{b + b'}$,那么我们结合引理 1 和引理 2,可得:
$$\mathbb E\left[\Phi_{t + 1}\right] \leq \mathbb E\left[\Phi_t - \frac\eta2\left\Vert\nabla f\left(x^t\right)\right\Vert^2\right]$$
同样的,将 $t$ 取遍 $0$ 到 $T - 1$。
$$\mathbb E\left[\left\Vert\nabla f\left(\hat x_T\right)\right\Vert^2\right] \leq \frac{2\Phi_0}T = \epsilon^2, \; \mathsf{\#grad} = b + T\left(pb + \left(1 - p\right)b'\right) = \mathcal O\left(b + \frac{\sqrt b}{\epsilon^2}\right)$$
其中,$b = n$。
我们看点图吧(
参考
https://proceedings.mlr.press/v139/li21a/li21a.pdf
Z1qqurat · 2024-07-27 17:18
Too strong
bb86 · 2024-07-27 15:19
👍👍