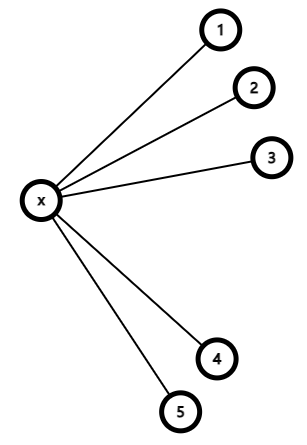
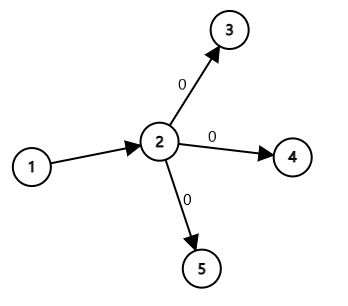
题意
给出一个网络图,以及其源点和汇点,求出其网络最大流。
题解
最大流问题就是,给你一张网络图,如果点 $u$ 到点 $v$ 有一条边,边权为 $w$,那么点 $u$ 到点 $v$ 最多 流 $w$ 的流量。求 汇点 最多能流到多少流量(源点流量无限)。
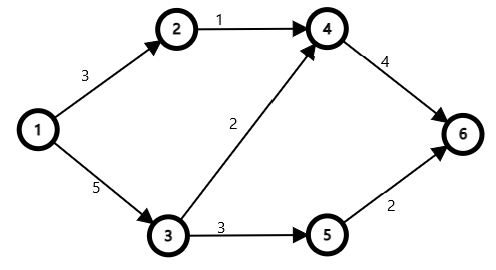
一个容易被想到的 错解
每次枚举一条从 源点 到 汇点 的路径,然后流 这条路径上所能流的最大流量。
Hack: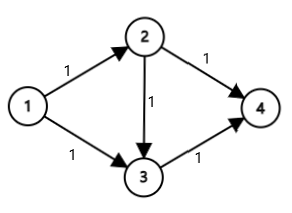
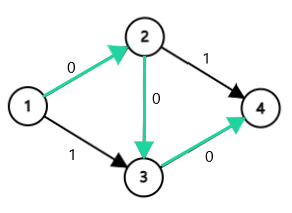
ford-fulkerson
如何把上面的算法改对呢?
维护退流。
即每次从 $u$ 到 $v$ 流 $w$ 的流量,就在反向边 $v$ 到 $u$ 也流 $w$ 的流量,这样做的意义就是让我们有反悔的机会。
ford-fulkerson 就是暴力 DFS 模拟增广过程。
复杂度 $\displaystyle \mathcal O(Fm)$,$F$ 就是最大流。
这个复杂度显然不太优,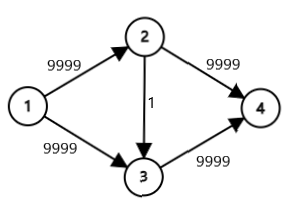
要是给它这张图跑的话,它就会跑 $20000$ 次。
dinic
如何改进 ford-fulkerson 呢?
每次只考虑增广到与 源点 距离差为 $1$ 的边。这样的话,
dinic 就会把中间那条边权为 $1$ 的边删除,这样流两次就搞定了。
优化
- 当前弧优化:
![]()
$1\ 2\ 3$ 是已经被 $x$ 访问过的点,现在 $4\ 5$ 要访问 $x$,那就不用在尝试给 $1\ 2\ 3$ 流量了,因为它们必然没有剩余流量。 - 炸点优化:
![]()
如果 $2$ 到汇点的路径上已经没有剩余流量了,就可以把 $2$ 炸掉,即以后再访问到 $2$ 时,立刻退出。
加上优化后 dinic 复杂度是 $\displaystyle \mathcal O(n^2m)$。
求方案
根据残量网络可以反推出方案。
代码:
#include <cstdint>
#include <cstring>
#include <iostream>
#include <list>
#include <unordered_map>
using namespace std;
using tp = int64_t;
constexpr tp Hat_N = 203, Hat_M = 5003;
tp s, t;
unordered_map<tp, tp> dep, head, to, next, mf;
void add(tp u, tp v, tp w) {
static tp cnt = 1;
to[++cnt] = v;
mf[cnt] = w;
::next[cnt] = head[u];
head[u] = cnt;
}
bool bfs() { // BFS 求出 源点 到 每个点 的距离
list<tp> q;
dep.clear();
dep[s] = 1;
for (q.push_back(s); q.size(); q.pop_front()) {
for (tp i = head[q.front()]; i; i = ::next[i]) {
if (!dep[to[i]] && mf[i]) {
dep[to[i]] = dep[q.front()] + 1;
q.push_back(to[i]);
}
}
}
return dep[t];
}
tp dfs(tp x, tp flow) {
tp tar = 0;
if (x == t) {
return flow;
}
for (tp i = head[x]; i && flow; i = ::next[i]) {
if (mf[i] && dep[to[i]] == dep[x] + 1) {
tp tf = dfs(to[i], min(flow, mf[i]));
mf[i] -= tf;
mf[i ^ 1] += tf; // 退流
flow -= tf;
tar += tf;
}
}
if (!tar) {
dep[x] = 0;
}
return tar;
}
tp dinic() {
tp tar = 0;
while (bfs()) {
tar += dfs(s, 0x7fffffffffffffff);
}
return tar;
}
signed main() {
tp n, m;
cin >> n >> m >> s >> t;
while (m--) {
tp u, v, w;
cin >> u >> v >> w;
add(u, v, w);
add(v, u, 0);
}
cout << dinic();
return 0;
}
// \
╭────────────────────────────────────────────────────────╮ \
│ This Code Was Created By RBTree (https://rbtr.ee/) │ \
╰────────────────────────────────────────────────────────╯
//