题意
有 $n + 1$ 辆巴士,编号为 $0$ 到 $n$,它们的速度都是固定的。前 $n$ 辆巴士有固定的出发时间。
在公路上,这些巴士不能超车(相对位置不能改变),所以当快的车追上慢的车之后,需要跟慢车保持同一速度行驶。
有 $m$ 个点,在这些点上可以超车(同一时间到这个点的车按照行驶速度排序,快车在前,慢车在后)。
现在有 $q$ 个询问,每次询问如果巴士 $n$ 从给定的点出发,到终点的时间是多少。
给两张图方便理解: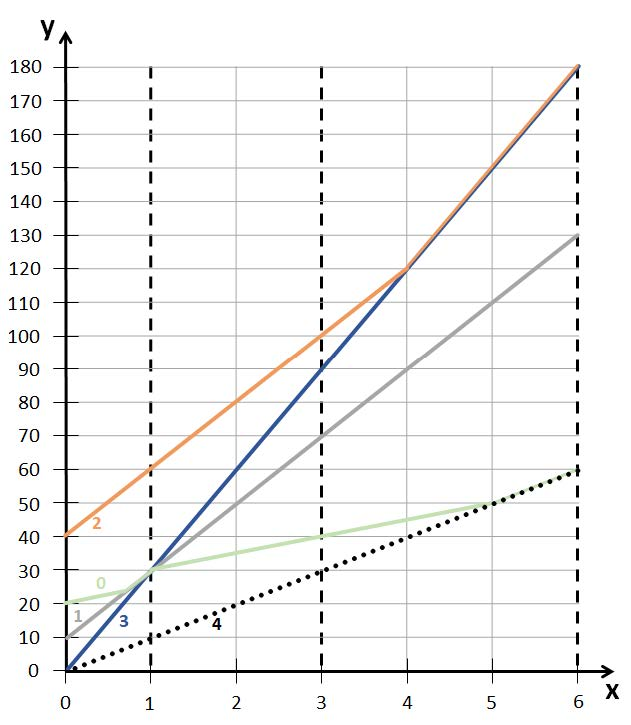
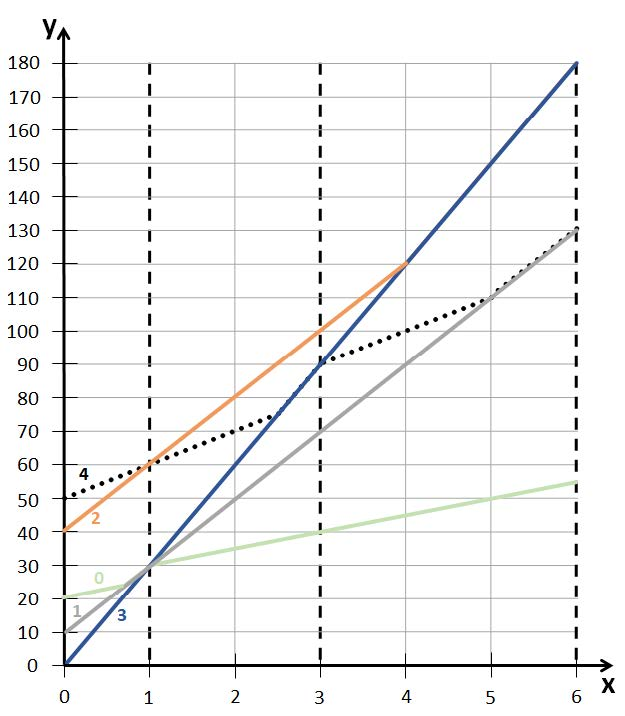
$1 \leq n, m \leq 10^3, 1 \leq q \leq 10^6$
题解
首先注意到,我们不需要管速度比巴士 $n$ 快的车,也不需要管在巴士 $n$ 后面的比它慢的车。它们都不会对巴士 $n$ 造成影响,因为巴士 $n$ 永远不会等它们。
于是,我们可以得到这样一个图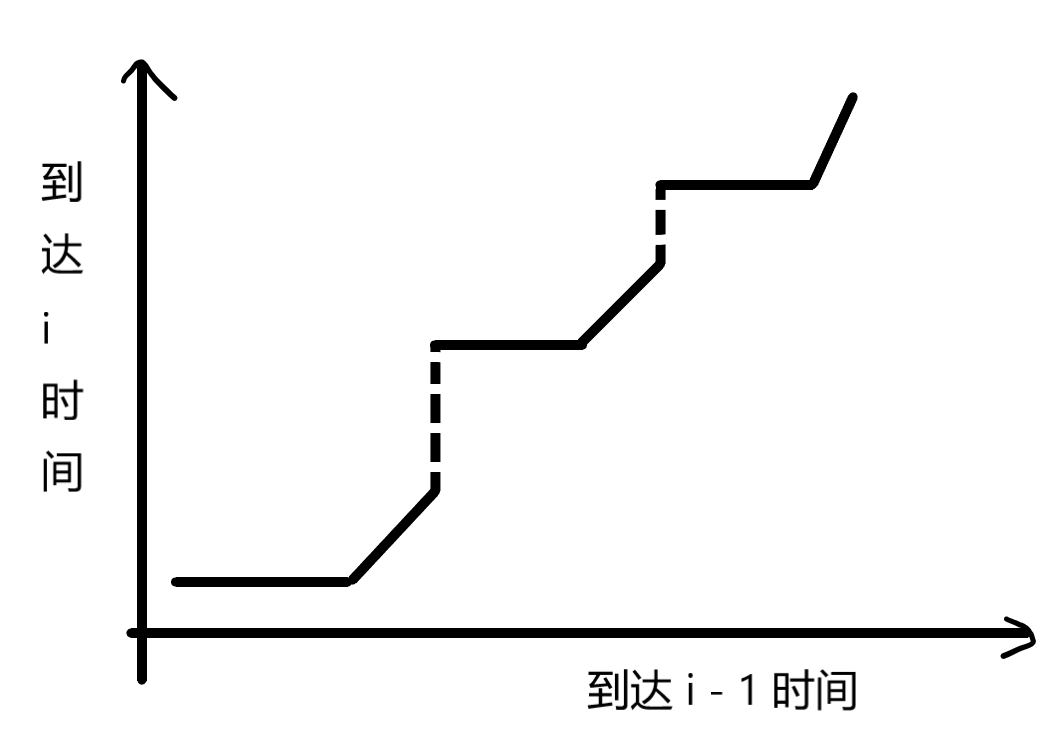
这是一个分段线性函数,分 $\mathcal O\left(n\right)$ 段。
直接维护这个函数。复杂度 $\mathcal O\left(nm \log n + q \log n\right)$