概述
计算几何主要解决 点、线、面 之间的位置和大小关系。
向量
向量是一个有大小和方向但不确定位置的量,但我们可以用 $\overrightarrow {AB}$ 表示一个从 $A$ 点到 $B$ 点的向量。另外 $\left\lvert AB \right\rvert$ 表示向量的模(又称模长,是向量的大小和长度)。
向量加法
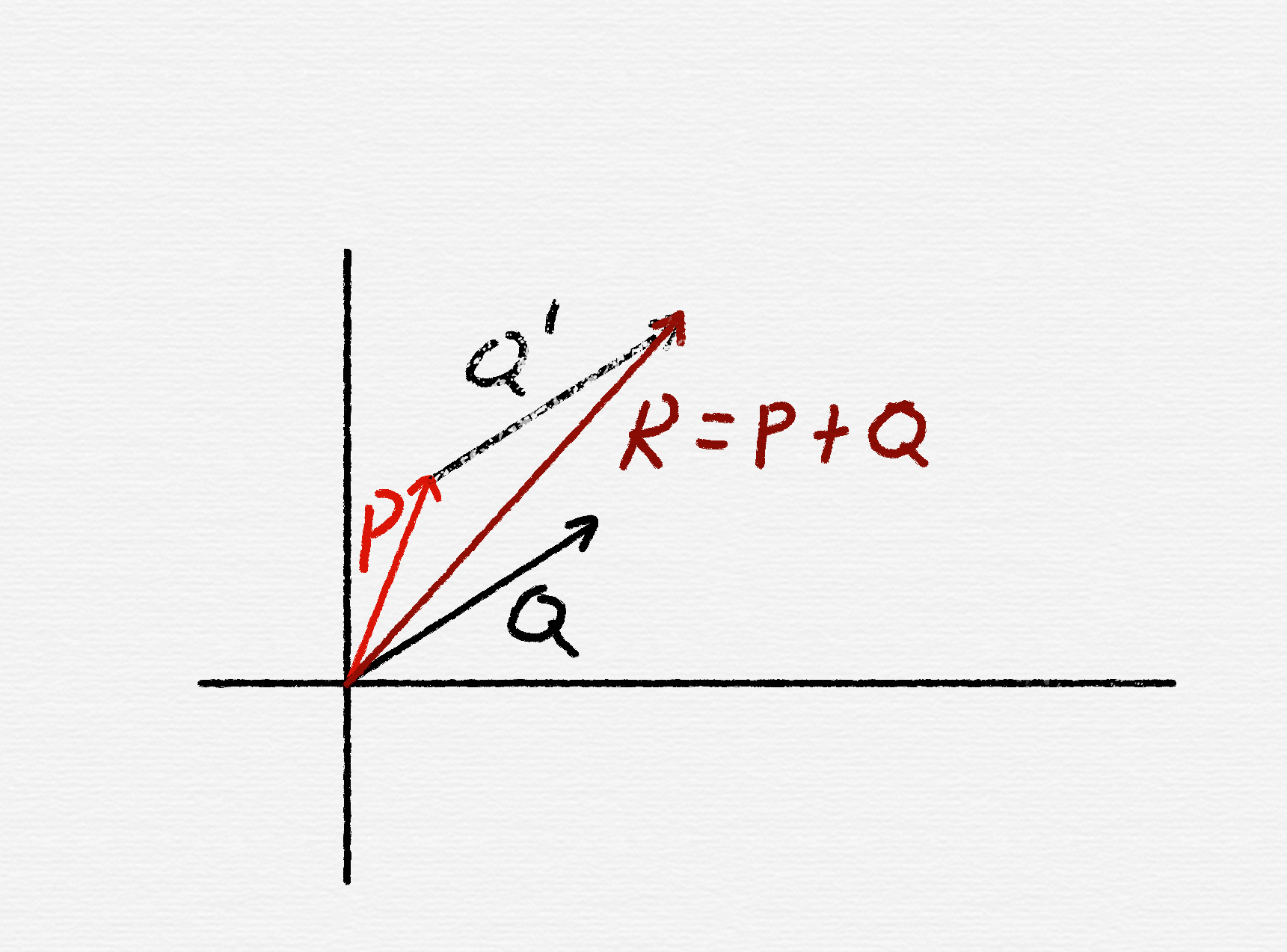
对每个维度分别相加,相当于将两个向量首尾相接。
设 $\vec P = \left(a, b\right), \vec Q = \left(c, d\right)$,则 $\vec R = \vec P + \vec Q = \left(a + c, b + d\right)$
向量减法
对每个维度分别相减,相当于被减向量加上减向量的反向量。
向量点乘
点乘符号为 $\cdot$。$\vec P \cdot \vec Q = \left\lvert P \right\rvert \left\lvert Q \right\rvert \cos\theta$,其中 $\theta$ 为 $\vec P$ 与 $\vec Q$ 的夹角。
点乘的结果被称为点积,又称内积,是标量。
设 $\vec P = \left(a, b\right), \vec Q = \left(c, d\right)$,则 $\vec P \cdot \vec Q = a \times c + b \times d$
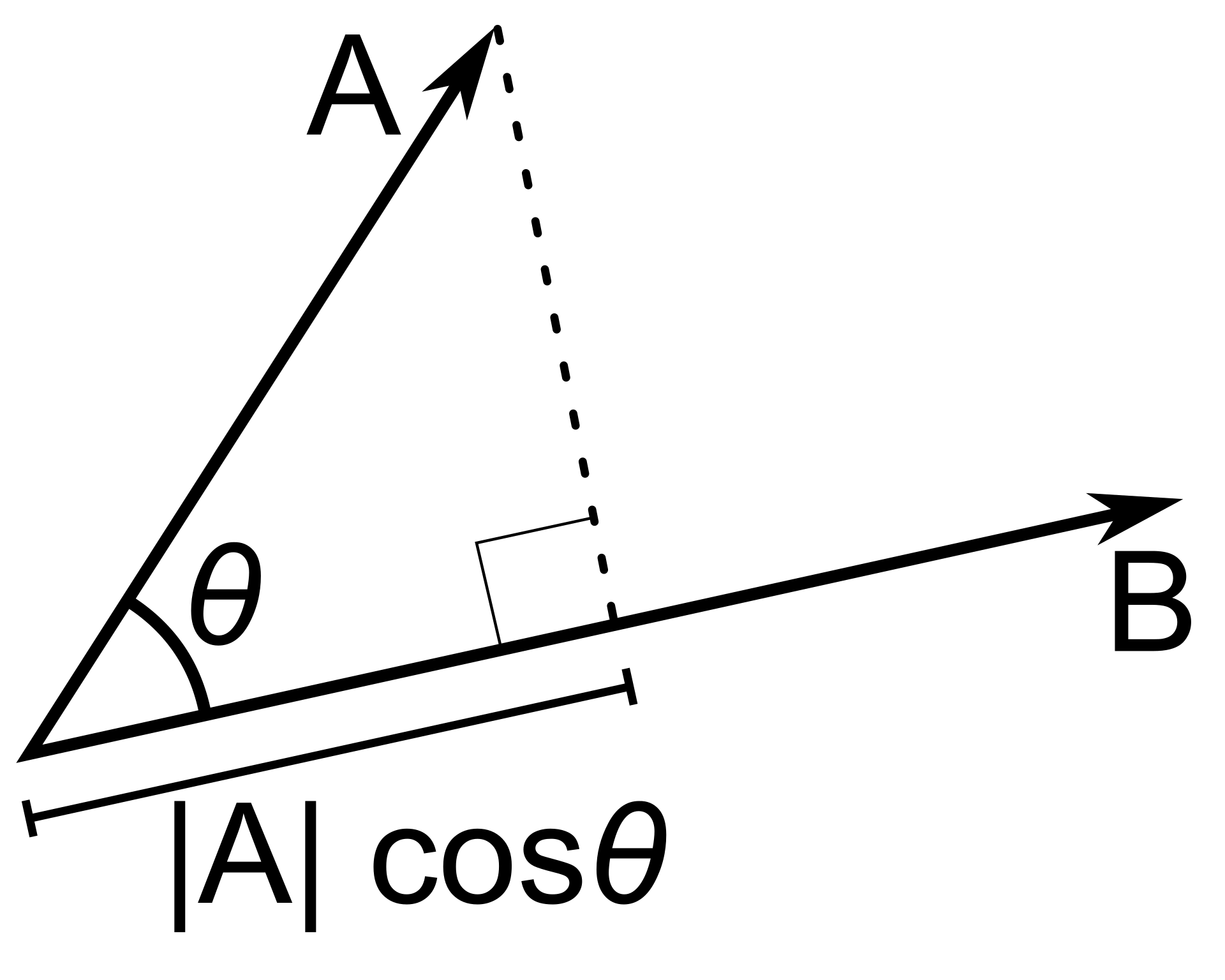
(此图来自 wikipedia)
点乘满足交换律。
点乘常用于判断向量的前后关系
- $\vec a \cdot \vec b > 0$:夹角为锐角
- $\vec a \cdot \vec b = 0$:夹角为直角
- $\vec a \cdot \vec b < 0$:夹角为钝角
向量叉乘
点乘符号为 $\times$。$\left\lvert\vec P \times \vec Q\right\rvert = \left\lvert P \right\rvert \left\lvert Q \right\rvert \sin\theta$,其中 $\theta$ 为 $\vec P$ 与 $\vec Q$ 的夹角。
点乘的结果被称为叉积,又称外积,是向量,该向量的方向用右手系得出,与坐标平面垂直,与 $Z$ 轴平行。
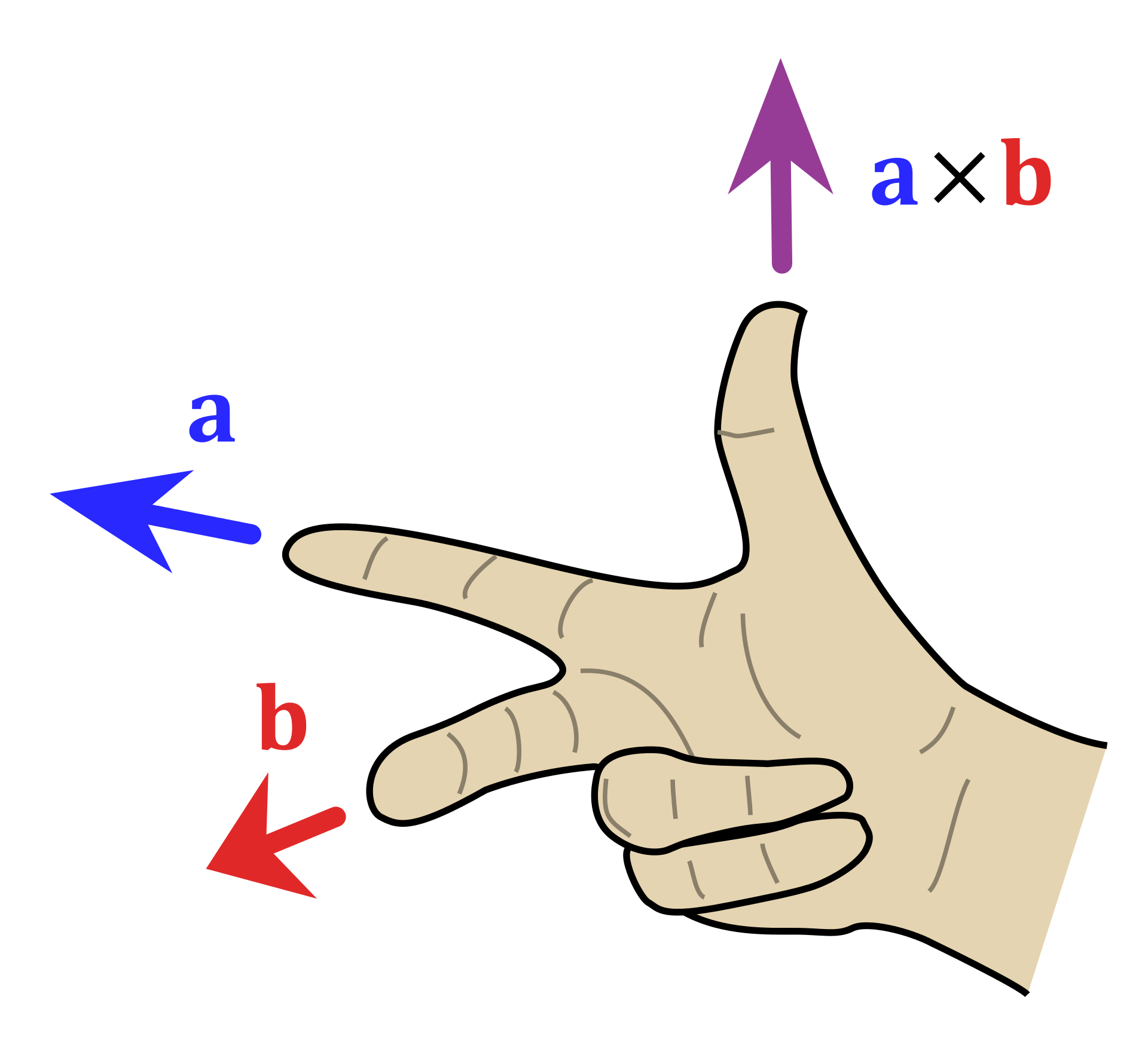
(此图来自 wikipedia)
设 $\vec P = \left(a, b\right), \vec Q = \left(c, d\right)$,则 $\left\lvert\vec P \cdot \vec Q \right\rvert = a \times d - b \times c$
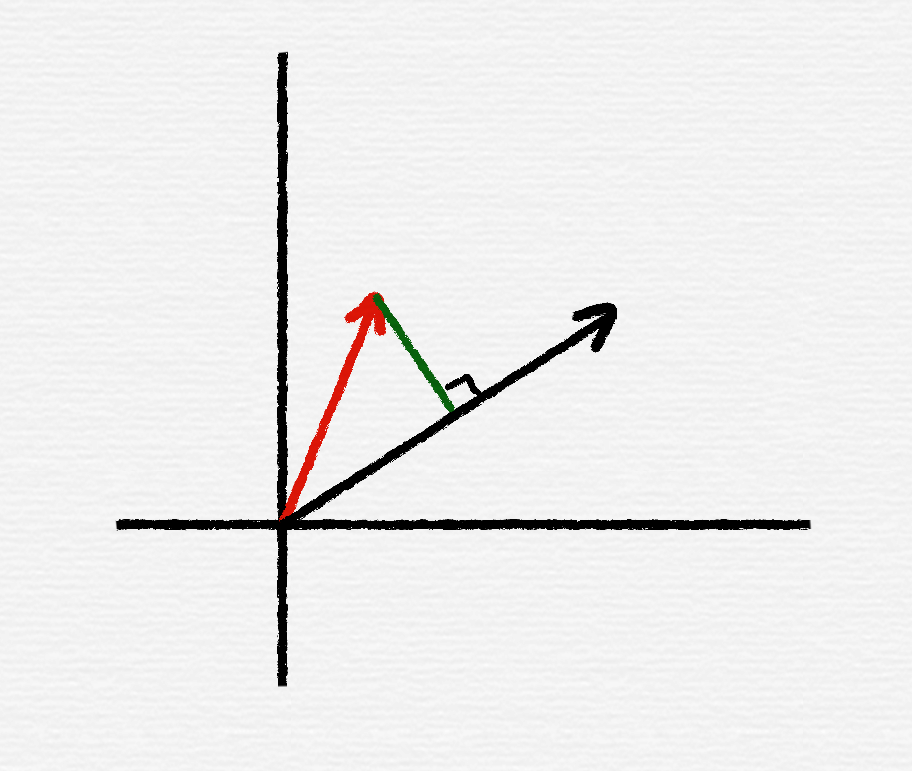
叉乘不满足交换律,交换后得出的结果与原结果互为相反数。
叉乘常用于判断向量的左右关系
- $\vec a \times \vec b > 0$:$\vec b$ 在 $\vec a$ 的逆时针方向
- $\vec a \times \vec b = 0$:两向量共线
- $\vec a \times \vec b < 0$:$\vec b$ 在 $\vec a$ 的顺时针方向
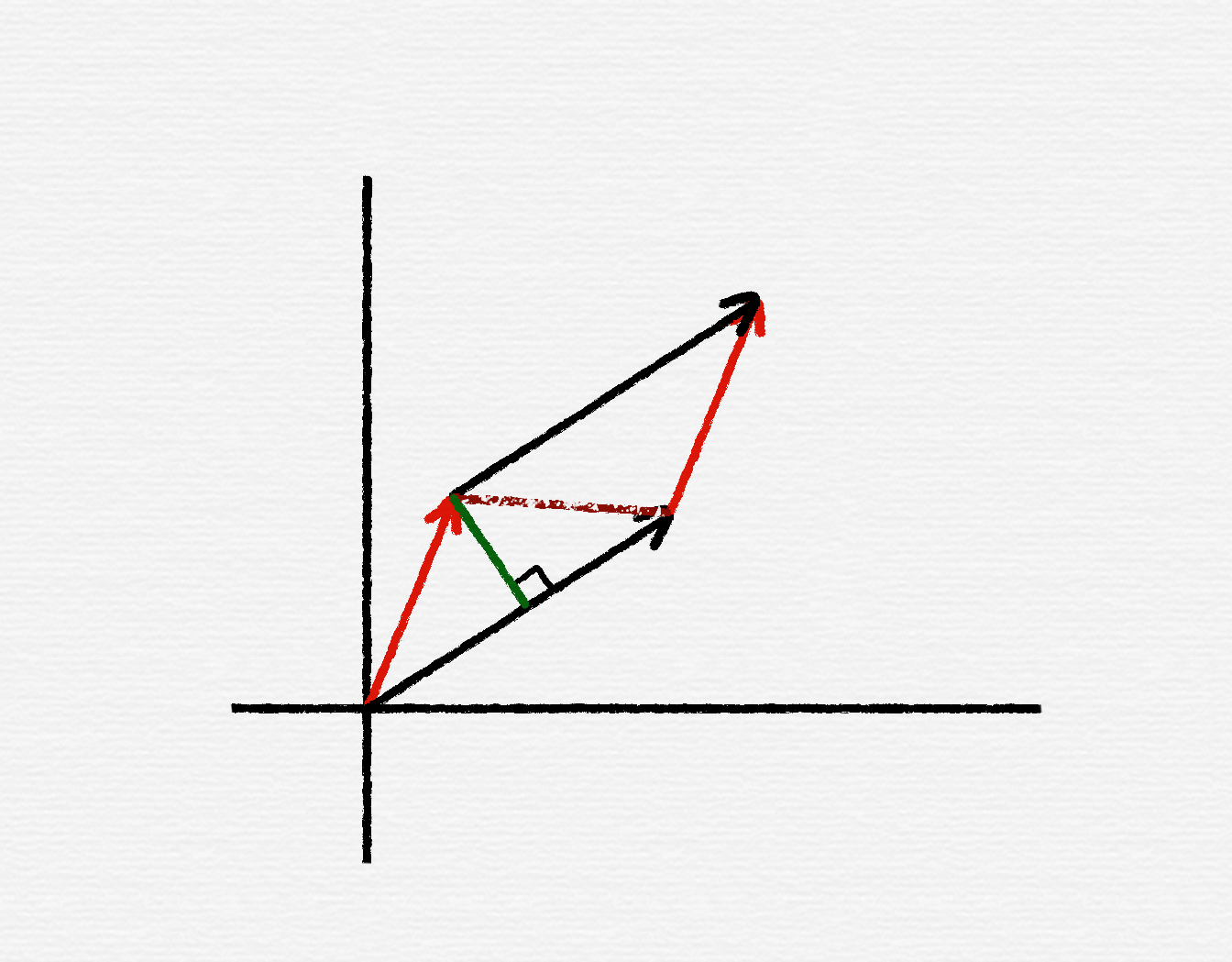
两向量叉积的模长等于两条向量构成的平行四边形的有向面积,因为三角形面积为 $\dfrac12ab\sin\theta$
射线法:点包含问题
射线法用于检测一个点是否在一个多边形内部。
从该点开始向某个方向作射线,检查该射线与多边形每一边的相交情况。如果是奇数说明该点在多边形内部, 还有在边上的情况需要特殊处理。注意判断该射线与某一边共线或交在拐点处的情况。最好的方法就是作一条斜率无穷小的射线,避免出现这些问题。
时间复杂度:$\Theta\left(n\right)$
// 2 : inside, 1 : on seg, 0: outside
tp contain(vector<Point> ps, Point p) {
tp n = ps.size(), ret = 0;
for (tp i = 0; i < n; ++i) {
Point u = ps[i], v = ps[(i + 1) % n];
if (OnSeg(u, v, p)) return 1;
if (cmp(u.y, v.y) <= 0) swap(u, v);
if (cmp(p.y, u.y) > 0 || cmp(p.y, v.y) <= 0) continue;
ret ^= CrossOp(p, u, v) > 0;
}
return ret * 2;
}旋转法:简单多边形面积
任选一点 $P$,按顺序枚举每多边形上两个相邻的顶点,累计三点围成的有向面积即可。不该算的面积被抵消掉,该算的恰好算了一遍。不好描述,拿个例子玩一玩就明白了。
时间复杂度:$\Theta\left(n\right)$
double area(vector<Point> ps) {
double ret = 0;
for (tp i = 0; i < ps.size(); ++i) res += cross(ps[i], ps[(i + 1) % n]);
return res / 2;
}二维凸包
定义:能包含所有点的最小凸多边形。
在非严格凸包中可以接受三点共线的情况。
我们的思路是先求上凸壳再求下凸壳,然后并起来。
首先维护一个栈,往里面不停丢点。

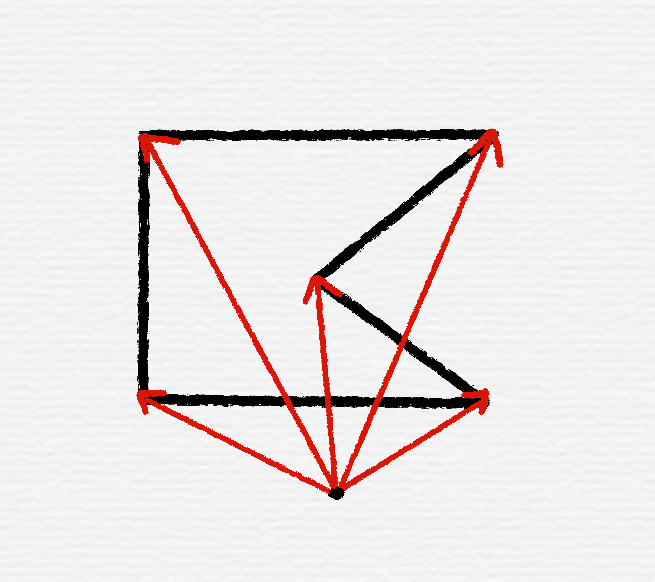
假设黑色的是我们当前的凸壳,现在要加入红点。现在红边与最后一条黑边不再构成顺时针旋转关系,于是将最后一个黑点弹出,再次检查。

若依然不满足旋转关系,就继续弹出最后一个黑点,直到满足。

然后把红点加入栈中。
此算法名为 Graham 算法,由于要排序,复杂度为 $\mathcal O\left(n \log n\right)$。
参考
https://en.wikipedia.org/wiki/Dot_product
https://en.wikipedia.org/wiki/Cross_product
https://oi.men.ci/geometry-notes/