概述
快速傅里叶变换(Fast Fourier Transform, FFT)可以在 $\Theta\left(n \log n\right)$ 的时间内计算多项式乘法。
但 FFT 的用处远不止于此。
多项式
一个多项式 $F\left(x\right) = a_0 + a_1x + a_2x^2 + \cdots$。
其中,$a_i$ 被称为 $F\left(x\right)$ 的 $i$ 次项系数。
多项式的点值表示法
$n + 1$ 个点可以唯一确定一个 $n$ 次多项式。可以使用 待定系数法 证明。
在某些情况下,使用点值表示法的多项式可以在线性复杂度内计算乘积。
给定两个 $n$ 次 $F\left(x\right)$ 和 $G\left(x\right)$:
他们的乘积 $\left(F * G\right)\left(x\right) = F\left(x\right) G\left(x\right)$。
因此,如果我们有 $k$ 个点 $x_1, x_2, \ldots, x_k$,并且知道 $F\left(x_1\right), F\left(x_2\right), \ldots, F\left(x_k\right)$ 和 $G\left(x_1\right), G\left(x_2\right), \ldots, G\left(x_k\right)$,那么我们就可以得到:
$$\left(F * G\right)\left(x_i\right) = F\left(x_i\right)G\left(x_i\right)$$
注意:因为 $\left(F * G\right)\left(x\right)$ 是一个 $2n$ 次的多项式,所以需要 $k = 2n + 1$ 个点才能确定。
把 系数表达 转换为 点值表达 称为 DFT(离散傅里叶变换)。
离散傅里叶变换
把 点值表达 转换为 系数表达 称为 IDFT(离散傅里叶逆变换)。
快速傅里叶变换 把 离散傅里叶变换 和 离散傅里叶逆变换 加速到了 $\mathcal O\left(n \log n\right)$。
虚数
虚数单位 $i$ 的定义为 $i = \sqrt{-1}$,即 $i^2 = -1$。
复数
复数定义为 $a + bi$。前项称为该复数的实部,后项称为该复数的虚部。
几何意义
实数的几何意义可以看作是数轴上的一个点。
而复数则可以看作平面上的一个点。我们把这个平面称为复平面。它的 $x$ 轴表示复数的实部,而 $y$ 轴表示复数的虚部。
具体来说:一个复数 $x = a + bi$ 可以看作 $\left(a, b\right)$ 这个点。
这个点也可以使用极坐标系来定义,我们把这个点到原点的距离(极径)叫做模长,写作 $\lvert x \rvert$。把原点到该点的射线与实轴正方向射线组成的角(逆时针旋转)的角度(极角)称为这个复数的幅角,写作 $\arg\left(x\right)$。
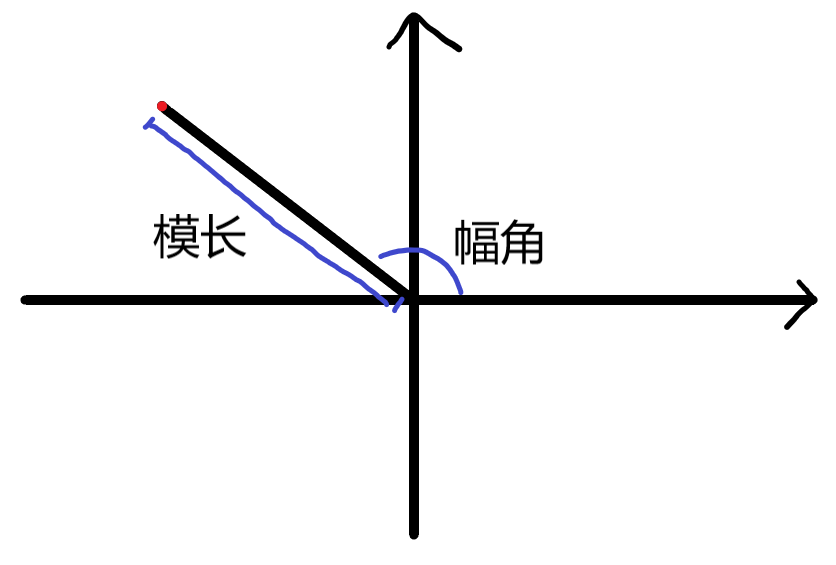
加法
实部 和 虚部 分别相加即可。
$\left(a + bi\right) + \left(c + di\right) = \left(a + c\right) + \left(b + d\right)i$
减法
实部 和 虚部 分别相加即可。
$\left(a + bi\right) - \left(c + di\right) = \left(a - c\right) + \left(b - d\right)i$
乘法
直接乘,然后暴力化简。
$\left(a + bi\right)\left(c + di\right) = ac + adi + bci + bdi^2 = ac + adi + bci - bd = \left(ac - bd\right) + \left(ad + bc\right)i$
几何意义:复数相乘时,模长相乘,幅角相加!
共轭
$\left(a + bi\right)\left(a - bi\right) = a^2 + b^2$
除法
直接乘,然后乱搞化简。
$\dfrac{a + bi}{c + di} = \dfrac{\left(a + bi\right)\left(c - di\right)}{\left(c + di\right)\left(c - di\right)} = \dfrac{\left(ac + bd\right) + \left(bc - ad\right)i}{c^2 + d^2} = \dfrac{ac + bd}{c^2 + d^2} + \dfrac{bc - ad}{c^2 + d^2}i$
单位根
定义
$n$ 次单位根,即方程 $x^n = 1$ 的复数解。
首先,单位圆定义为一个以原点为圆心,半径为 $1$ 的圆:
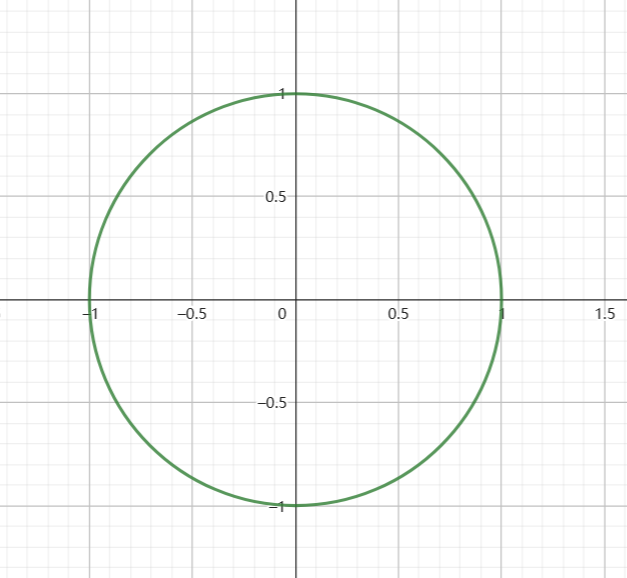
在这个单位圆上的点表示的复数的模长都是 $1$。
如果一个复数 $x$ 的模长大于 $1$,那么 $\lvert x^n \rvert = \lvert x \rvert^n > 1$。
如果一个复数 $x$ 的模长小于 $1$,那么 $\lvert x^n \rvert = \lvert x \rvert^n < 1$。
所以只有模长等于 $1$ 的复数才有可能成为 $n$ 次单位根。
在圆上的复数的模长都是 $1$,接下来考虑幅角。
容易找到幅角为 $0, \dfrac{2\pi}n, \dfrac{4\pi}n, \ldots \dfrac{2\pi\left(n - 1\right)}n$ 的复数,就是单位根。而根据代数基本定理:$n$ 次方程在复数域内有且只有 $n$ 个根。
$n$ 次单位根也可以定义为 $e^\dfrac{2\pi i}{n}$。
容易知道这玩意的 $n$ 次方幅角是圆周的若干倍,那么就和 $1$ 重合。
比如,$3$ 次单位根就长这样:

当然,单位根也有符号。第 $i$ 个 $n$ 次单位根:$\omega_n^i$
性质
- $\omega_n^0 = 1$
- $\omega_n^k \cdot \omega_n^j = \omega_n^{k + j}$:感性理解就是在单位圆上转。也可以套公式获得严格证明。
- $\omega_{2n}^{2k} = \omega_n^k$:把圆分成 $2n$ 份取 $2k$ 份跟把圆分成 $n$ 份取 $k$ 份是一样的。
- 如果 $n$ 是偶数,$\omega_n^{k + n / 2}=-\omega_n^k$:相当于转了半个圆,那就走到了跟当前位置完全相反的那个点上。
快速傅里叶变换
现在有多项式 $F\left(x\right) = a_0 + a_1x + a_2x^2 + a_3x^3 + \cdots$,我们想加速离散傅里叶变换。
首先,我们要做的,是把 $F\left(x\right)$ 的奇数次项和偶数次项分开考虑。
设 $G\left(x\right) = a_0 + a_2x + a_4x^2 + \cdots$,$H\left(x\right) = a_1 + a_3x + a_5x^2 + \cdots$。这里保证 $F\left(x\right)$ 的项数是 $2$ 的整数次幂。不会出现分不匀的情况。
现在,$F\left(x\right)$ 可以写作 $G\left(x^2\right) + xH\left(x^2\right)$。
把 $\omega_n^k$ 代入 $F\left(x\right)$:
$$ \begin{aligned} F\left(\omega_n^k\right) &= G\left(\left(\omega_n^k\right)^2\right) + \omega_n^k H\left(\left(\omega_n^k\right)^2\right)\\ &= G\left(\omega_{n / 2}^k\right) + \omega_n^k H\left(\omega_{n / 2}^k\right) \end{aligned} $$
而把 $\omega_n^{k + n / 2}$ 代入 $F\left(x\right)$:
$$ \begin{aligned} F\left(\omega_n^{k + n / 2}\right) &= G\left(\left(\omega_n^{k + n / 2}\right)^2\right) + \omega_n^{k + n / 2} H\left(\left(\omega_n^{k + n / 2}\right)^2\right)\\ &= G\left(\omega_n^{2k + n}\right) + \omega_n^{k + n / 2} H\left(\omega_n^{2k + n}\right)\\ &= G\left(\omega_n^{2k}\right) + \omega_n^{k + n / 2} H\left(\omega_n^{2k}\right)\\ &= G\left(\omega_{n / 2}^k\right) + \omega_n^{k + n / 2} H\left(\omega_{n / 2}^k\right)\\ &= G\left(\omega_{n / 2}^k\right) - \omega_n^k H\left(\omega_{n / 2}^k\right) \end{aligned} $$
把两个式子放在一起看看:
$$ \begin{aligned} F\left(\omega_n^k\right) &= G\left(\omega_{n / 2}^k\right) + \omega_n^k H\left(\omega_{n / 2}^k\right) \\ F\left(\omega_n^{k + n / 2}\right) &= G\left(\omega_{n / 2}^k\right) - \omega_n^k H\left(\omega_{n / 2}^k\right) \end{aligned} $$
就只有一个正负号的区别!
如果我们知道两个多项式 $G\left(x\right)$ 和 $H\left(x\right)$ 分别在 $\omega^0_{n/2}, \omega^1_{n / 2}, \omega^2_{n / 2}, \ldots, \omega^{n / 2 - 1}_{n / 2}$ 的点值表示,
根据 $F\left(\omega_n^k\right) = G\left(\omega_{n / 2}^k\right) + \omega_n^k H\left(\omega_{n / 2}^k\right)$,我们可以在线性复杂度内求出 $F\left(x\right)$ 在 $\omega^0_n, \omega^1_n, \omega^2_n, \ldots, \omega^{n / 2 - 1}_n$ 处的点值表示。
根据 $F\left(\omega_n^{k + n / 2}\right) = G\left(\omega_{n / 2}^k\right) - \omega_n^k H\left(\omega_{n / 2}^k\right)$ 我们可以在线性复杂度内求出 $F\left(x\right)$ 在 $\omega^{n / 2}_n, \omega^{n / 2 + 1}_n, \omega^{n / 2 + 2}_n, \ldots, \omega^{n - 1}_n$ 处的点值表示。
所以如果我们知道两个多项式 $G\left(x\right)$ 和 $H\left(x\right)$ 分别在 $\omega^0_{n/2}, \omega^1_{n / 2}, \omega^2_{n / 2}, \ldots, \omega^{n / 2 - 1}_{n / 2}$ 的点值表示,我们就可以在线性复杂度内求出 $F\left(x\right)$ 在 $\omega^0_n, \omega^1_n, \omega^2_n, \ldots, \omega^{n - 1}_n$ 处的点值表示。
由于计算 $G\left(x\right)$ 和 $H\left(x\right)$ 跟求 $F\left(x\right)$ 的流程是同样的,所以我们可以递归去求。
得到复杂度的递归式为 $T\left(n\right) = 2T\left(n / 2\right) + \Theta\left(n\right)$,根据主定理,$T\left(n\right) = \Theta\left(n \log n\right)$。
我们就在 $\Theta\left(n \log n\right)$ 的复杂度内成功获得了 $F\left(x\right)$ 的点值表示。
实现
首先,我们要保证 $F\left(x\right)$ 的项数是 $2$ 的整数次幂。因此要在后面添加系数为 $0$ 的项。
然后就是求单位根的事了。我们知道 $\omega_n^k = \left(\omega_n^1\right)^k$,所以只需要知道 $\omega_n^1$ 即可。
通过一些三角函数知识可以知道:
$$\omega_n^1 = \cos\left(\frac{2\pi}n\right) + \sin\left(\frac{2\pi}n\right)i$$
struct Complex {
double r, i;
Complex() = default;
Complex(double x, double y) : r(x), i(y) {}
Complex operator+(Complex const& b) const { return Complex(r + b.r, i + b.i); }
Complex operator-(Complex const& b) const { return Complex(r - b.r, i - b.i); }
Complex operator*(Complex const& b) const { return Complex(r * b.r - i * b.i, r * b.i + i * b.r); }
Complex operator/(Complex const& b) const {
double t = b.r * b.r + b.i * b.i;
return Complex((r * b.r + i * b.i) / t, (i * b.r - r * b.i) / t);
}
Complex operator+=(Complex const& b) { return *this = *this + b; }
Complex operator-=(Complex const& b) { return *this = *this - b; }
Complex operator*=(Complex const& b) { return *this = *this * b; }
Complex operator/=(Complex const& b) { return *this = *this / b; }
};struct Complex{double r,i;Complex()=default;Complex(double x,double y):r(x),i(y){}Complex operator+(Complex const&b)const{return Complex(r+b.r,i+b.i);}Complex operator-(Complex const&b)const{return Complex(r-b.r,i-b.i);}Complex operator*(Complex const&b)const{return Complex(r*b.r-i*b.i,r*b.i+i*b.r);}Complex operator/(Complex const&b)const{double t=b.r*b.r+b.i*b.i;return Complex((r*b.r+i*b.i)/t,(i*b.r-r*b.i)/t);}Complex operator+=(Complex const&b){return*this=*this+b;}Complex operator-=(Complex const&b){return*this=*this-b;}Complex operator*=(Complex const&b){return*this=*this*b;}Complex operator/=(Complex const&b){return*this=*this/b;}};vector<Complex> w(n); // omega
w[0] = Complex(1, 0);
w[1] = Complex(cos(2 * acos(-1) / n), sin(2 * acos(-1) / n));
for (tp i = 2; i < n; ++i) w[i] = w[i - 1] * w[1];
for (tp i = 0; i < n; ++i) bin << i << ' ' << w[i].r << ' ' << w[i].i << '\n';vector<Complex> f, tmp;
void FFT(vector<Complex>::iterator f, tp len) {
if (len == 1) return;
vector<Complex>::iterator g = f, h = f + len / 2;
for (tp k = 0; k < len; ++k) tmp[k] = f[k];
for (tp k = 0; k < len / 2; ++k) { g[k] = tmp[k * 2]; h[k] = tmp[k * 2 + 1];}
FFT(g, len / 2);
FFT(h, len / 2);
Complex w(cos(2 * acos(-1) / len), sin(2 * acos(-1) / len)), p(1, 0);
for (tp k = 0; k < len / 2; ++k) {
tmp[k] = g[k] + p * h[k];
tmp[k + len / 2] = g[k] - p * h[k];
p *= w;
}
for (tp k = 0; k < len; ++k) f[k] = tmp[k];
}
void STRUGGLING([[maybe_unused]] unsigned TEST_NUMBER) {
tp n, m = 1; bin >> n;
while (m < n) m *= 2;
f = tmp = vector<Complex>(m, Complex());
for (tp i = 0; i < n; ++i) bin >> f[i].r;
FFT(f.begin(), m);
for (tp i = 0; i < m; ++i) bin << f[i].r << ' ' << f[i].i << '\n';
}这样,我们就写完了 FFT。
快速傅里叶逆变换
这里直接给出结论:
把 FFT 中的 $\omega_n^1$ 换成 $\omega_n^{-1}$,做完之后除以 $n$ 即可。
证明平凡。
void IFFT(vector<Complex>::iterator f, tp len) {
if (len == 1) return;
vector<Complex>::iterator g = f, h = f + len / 2;
for (tp k = 0; k < len; ++k) tmp[k] = f[k];
for (tp k = 0; k < len / 2; ++k) { g[k] = tmp[k * 2]; h[k] = tmp[k * 2 + 1];}
IFFT(g, len / 2);
IFFT(h, len / 2);
Complex w(cos(2 * acos(-1) / len), -sin(2 * acos(-1) / len)), p(1, 0);
for (tp k = 0; k < len / 2; ++k) {
tmp[k] = g[k] + p * h[k];
tmp[k + len / 2] = g[k] - p * h[k];
p *= w;
}
for (tp k = 0; k < len; ++k) f[k] = tmp[k];
}多项式乘法
vector<Complex> f, tmp;
void FFT(vector<Complex>::iterator f, tp len, tp type) {
if (len == 1) return;
vector<Complex>::iterator g = f, h = f + len / 2;
for (tp k = 0; k < len; ++k) tmp[k] = f[k];
for (tp k = 0; k < len / 2; ++k) { g[k] = tmp[k * 2]; h[k] = tmp[k * 2 + 1];}
FFT(g, len / 2, type);
FFT(h, len / 2, type);
Complex w(cos(2 * acos(-1) / len), type * sin(2 * acos(-1) / len)), p(1, 0);
for (tp k = 0; k < len / 2; ++k) {
tmp[k] = g[k] + p * h[k];
tmp[k + len / 2] = g[k] - p * h[k];
p *= w;
}
for (tp k = 0; k < len; ++k) f[k] = tmp[k];
}
void STRUGGLING([[maybe_unused]] unsigned TEST_NUMBER) {
tp n, m, k = 1; bin >> n >> m;
while (k <= n + m) k *= 2;
f = g = tmp = vector<Complex>(k, Complex());
for (tp i = 0; i <= n; ++i) bin >> f[i].r;
for (tp i = 0; i <= m; ++i) bin >> g[i].r;
FFT(f.begin(), k, 1); FFT(g.begin(), k, 1);
for (tp i = 0; i < k; ++i) f[i] *= g[i];
FFT(f.begin(), k, -1);
for (tp i = 0; i <= n + m; ++i) bin << tp(f[i].r / k + 0.5) << ' ';
bin << '\n';
}根据这个方法,我们可以得到一个 $\frac23$ 常数的 FFT:
vector<Complex> f, tmp;
void FFT(vector<Complex>::iterator f, tp len, tp type) {
if (len == 1) return;
vector<Complex>::iterator g = f, h = f + len / 2;
for (tp k = 0; k < len; ++k) tmp[k] = f[k];
for (tp k = 0; k < len / 2; ++k) { g[k] = tmp[k * 2]; h[k] = tmp[k * 2 + 1];}
FFT(g, len / 2, type);
FFT(h, len / 2, type);
Complex w(cos(2 * acos(-1) / len), type * sin(2 * acos(-1) / len)), p(1, 0);
for (tp k = 0; k < len / 2; ++k) {
tmp[k] = g[k] + p * h[k];
tmp[k + len / 2] = g[k] - p * h[k];
p *= w;
}
for (tp k = 0; k < len; ++k) f[k] = tmp[k];
}
void STRUGGLING([[maybe_unused]] unsigned TEST_NUMBER) {
tp n, m, k = 1; bin >> n >> m;
while (k <= n + m) k *= 2;
f = tmp = vector<Complex>(k, Complex());
for (tp i = 0; i <= n; ++i) bin >> f[i].r;
for (tp i = 0; i <= m; ++i) bin >> f[i].i;
FFT(f.begin(), k, 1);
for (tp i = 0; i < k; ++i) f[i] *= f[i];
FFT(f.begin(), k, -1);
for (tp i = 0; i <= n + m; ++i) bin << tp(f[i].i / 2 / k + 0.5) << ' ';
bin << '\n';
}再使用蝴蝶变换:
void FFT(vector<Complex>::iterator f, tp len, tp type) {
if (len == 1) return;
FFT(f, len / 2, type);
FFT(f + len / 2, len / 2, type);
Complex w(cos(2 * acos(-1) / len), type * sin(2 * acos(-1) / len)), p(1, 0);
for (tp k = 0; k < len / 2; ++k) {
Complex t = p * f[k + len / 2];
f[k + len / 2] = f[k] - t;
f[k] += t;
p *= w;
}
}
void STRUGGLING([[maybe_unused]] unsigned TEST_NUMBER) {
tp n, m, k = 1; bin >> n >> m;
while (k <= n + m) k *= 2;
vector<Complex> f(k, Complex());
vector<tp> bf(k, 0);
for (tp i = 0; i <= n; ++i) bin >> f[i].r;
for (tp i = 0; i <= m; ++i) bin >> f[i].i;
for (tp i = 0; i < k; ++i) bf[i] = (bf[i / 2] / 2) | (i % 2 * k / 2);
for (tp i = 0; i < k; ++i) {
if (i < bf[i]) swap(f[i], f[bf[i]]);
}
FFT(f.begin(), k, 1);
for (tp i = 0; i < k; ++i) f[i] *= f[i];
for (tp i = 0; i < k; ++i) {
if (i < bf[i]) swap(f[i], f[bf[i]]);
}
FFT(f.begin(), k, -1);
for (tp i = 0; i <= n + m; ++i) bin << tp(f[i].i / 2 / k + 0.5) << ' ';
bin << '\n';
}写成非递归形式:
void FFT(vector<Complex>::iterator f, tp n, tp type) {
double pi2 = acos(-1) * 2;
vector<tp> bf(n, 0);
for (tp i = 0; i < n; ++i) bf[i] = (bf[i / 2] / 2) | (i % 2 * n / 2);
for (tp i = 0; i < n; ++i) {
if (i < bf[i]) swap(f[i], f[bf[i]]);
}
for (tp p = 2; p <= n; p *= 2) {
tp m = p / 2;
Complex w(cos(pi2 / p), type * sin(pi2 / p));
for (tp k = 0; k < n; k += p) {
Complex g(1, 0);
for (tp l = k; l < k + m; ++l) {
Complex t = g * f[m + l];
f[m + l] = f[l] - t;
f[l] += t;
g *= w;
}
}
}
if (type == 1) return;
for (tp i = 0; i < n; ++i) f[i].r /= n;
for (tp i = 0; i < n; ++i) f[i].i /= n;
}
void STRUGGLING([[maybe_unused]] unsigned TEST_NUMBER) {
tp n, m, k = 1; bin >> n >> m;
while (k <= n + m) k *= 2;
vector<Complex> f(k, Complex());
for (tp i = 0; i <= n; ++i) bin >> f[i].r;
for (tp i = 0; i <= m; ++i) bin >> f[i].i;
FFT(f.begin(), k, 1);
for (tp i = 0; i < k; ++i) f[i] *= f[i];
FFT(f.begin(), k, -1);
for (tp i = 0; i <= n + m; ++i) bin << tp(f[i].i / 2 + 0.5) << ' ';
bin << '\n';
}施工中。。。