Sliding Window Advertisement
A fence consists of $n$ vertical boards. The width of each board is $1$ and their heights may vary.
You want to attach a rectangular advertisement to the fence. Your task is to calculate the maximum area of such an advertisement in each window of $k$ vertical boards, from left to right.
$1 \leq k \leq n \leq 2 \times 10^5$
$1 \leq x_i \leq 10^9$
Tutorial
For a range $\left[l, r\right]$, the maximum area we can obtain is $\left(r - l + 1\right) \cdot \min\limits_{l \leq i \leq r}a_i$.
The first idea is to enumerate some ranges then compute the minimum value in the range. However, we find out that this method cannot be optimized any more, because the range length is not fixed.
Therefore, we consider another method: treat each $a_i$ as the minimum value and update the answer for the corresponding ranges.
The first step is to compute the range $\left[l_i, r_i\right]$ for each $a_i$ such that $a_i$ is the minimum value within this range. We can scan all values in decreasing order and use a std::set to track all positions where the value is less than the current one.
Then, for the range $\left[i, i + k - 1\right]$, if we choose $a_j$ as the minimum value, the resulting rectangle has an area of $\left(\min\left(i + k - 1, r_j\right) - \max\left(i, l_j\right) + 1\right) \times a_i$:
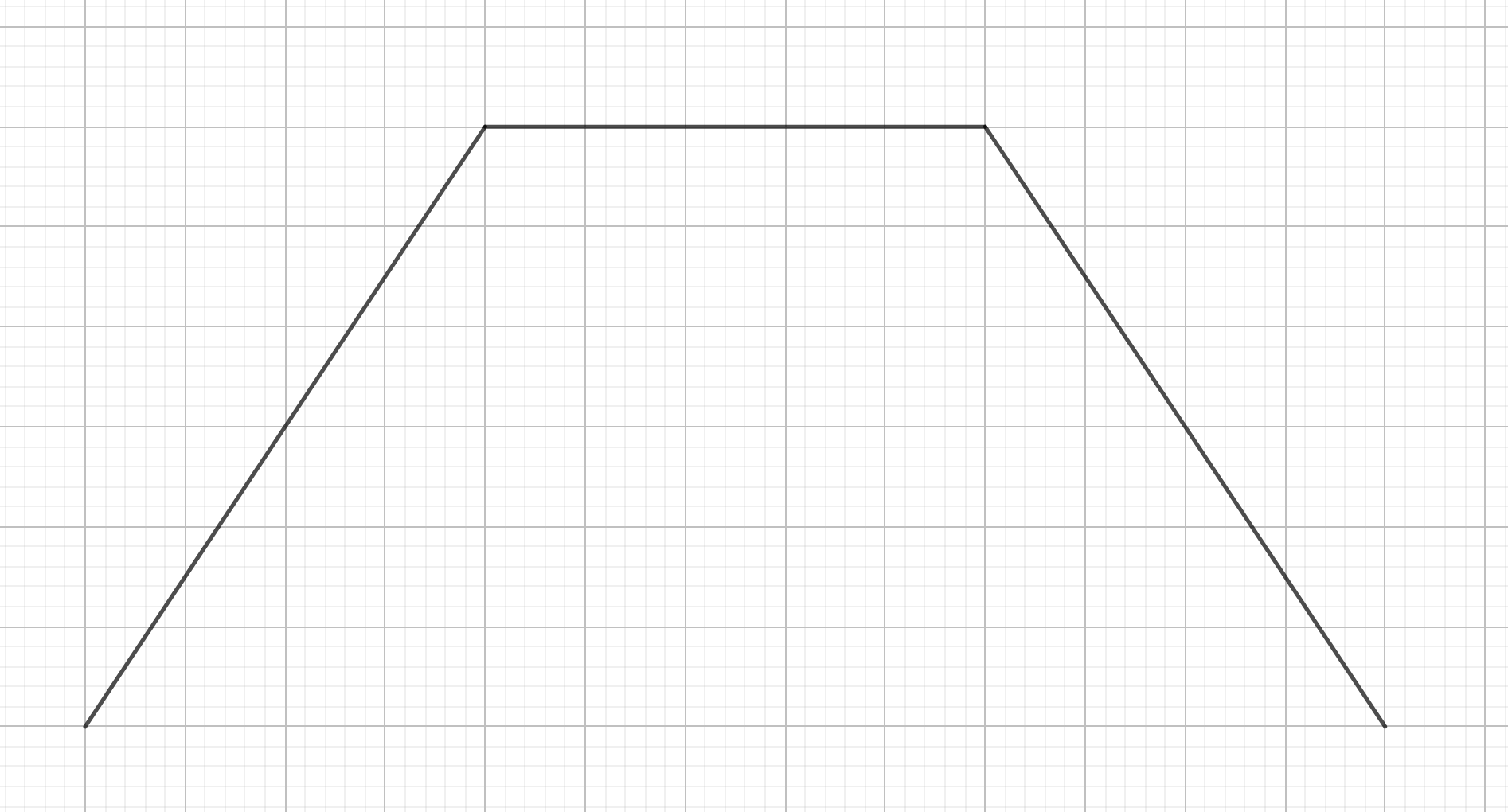
This shape can be split into three line segments with slopes of $a_i$, $0$ and $-a_i$, respectively.
Our goal is to compute the maximum value at each position $i \in \left[1, n - k + 1\right]$. Therefore, we can use a Li Chao Tree to maintain these line segments in $O\left(n \log n\right)$ time.
Code
// rbtree (https://rbtr.ee)
// n@rbtr.ee
#include "bits/stdc++.h"
constexpr char __FIO__[] = "";
constexpr char __FIN__[] = "";
constexpr char __FOUT__[] = "";
constexpr bool MTS = false;
constexpr bool SPC_MTS = false;
using ll = long long int;
using vl = std::vector<ll>;
using vi = std::vector<int>;
using pll = std::pair<ll, ll>;
using pil = std::pair<int, ll>;
using pli = std::pair<ll, int>;
using pii = std::pair<int, int>;
using bsl = std::basic_string<ll>;
using ull = unsigned long long int;
using bsi = std::basic_string<int>;
void SNOWFLAKE(int c, char* v[], int i);
static constexpr int INF32 = 0x3ffffffe;
static constexpr ll INF64 = 0x3ffffffffffffffe;
int main(int argc, char* argv[]) { if (strlen(__FIO__) !=0){freopen((std::string
(__FIO__) + ".in").c_str(), "r", stdin); freopen((std::string(__FIO__) + ".out")
.c_str(), "w",stdout);} else { if(strlen(__FIN__)!=0)freopen(__FIN__,"r",stdin);
if (strlen(__FOUT__) != 0) freopen(__FOUT__, "w",stdout);std::cin.tie(nullptr)->
sync_with_stdio(false); } int t = 1; if(MTS&&!SPC_MTS)std::cin>>t;try{for(int i=
1; i <= t || SPC_MTS; ++i) SNOWFLAKE(argc, argv, i); } catch (...) {} return 0;}
// :/
// :/
struct LineTree {
struct TNode {
ll k, b;
TNode *l, *r;
TNode() : k(0), b(0), l(nullptr), r(nullptr) {}
};
TNode* root;
int dl;
int dr;
bool comp(ll ak, ll ab, ll bk, ll bb, ll x) { return ak * x + ab > bk * x + bb; }
void _modify(TNode*& p, ll k, ll b, int l, int r, int ml, int mr) {
if (p == nullptr) p = new TNode();
int mid = (l + r) / 2;
if (ml <= l && r <= mr) {
if (l == r) {
if (comp(k, b, p->k, p->b, l)) p->k = k, p->b = b;
return;
}
if (comp(k, b, p->k, p->b, mid)) std::swap(p->k, k), std::swap(p->b, b);
if (comp(k, b, p->k, p->b, l)) _modify(p->l, k, b, l, mid, ml, mr);
if (comp(k, b, p->k, p->b, r)) _modify(p->r, k, b, mid + 1, r, ml, mr);
} else {
if (mid >= ml) _modify(p->l, k, b, l, mid, ml, mr);
if (mid < mr) _modify(p->r, k, b, mid + 1, r, ml, mr);
}
}
ll _query(TNode*& p, int pos, int l, int r) {
if (p == nullptr) return 0;
if (l == r) return p->k * pos + p->b;
int mid = (l + r) / 2;
ll ret = p->k * pos + p->b;
if (pos <= mid) ret = std::max(ret, _query(p->l, pos, l, mid));
else ret = std::max(ret, _query(p->r, pos, mid + 1, r));
return ret;
}
public:
LineTree(int dl, int dr) : dl(dl), dr(dr), root(new TNode()) {}
void modify(ll k, ll b, int l, int r) { _modify(root, k, b, dl, dr, l, r); }
ll query(int pos) { return _query(root, pos, dl, dr); }
};
struct SNOWFLAKE {
SNOWFLAKE(int argc, char* argv[], int TEST_NUMBER) {
int n, k; std::cin >> n >> k;
bsi a(n, 0);
for (auto& i : a) std::cin >> i;
std::map<int, bsi> app;
for (int i = 0; i < n; ++i) app[a[i]].push_back(i);
std::set<int> o;
for (int i = -1; i <= n; ++i) o.insert(i);
LineTree lt(0, n);
for (auto [v, p] : app | std::views::reverse) {
for (auto i : p) o.erase(i);
for (auto i : p) {
auto it = o.upper_bound(i);
int l = *prev(it) + 1;
int r = *it - 1;
if (r - k + 1 >= 0) {
lt.modify(v, ll(k - l) * v, std::max(0, l - k + 1), std::min(l, r - k + 1));
}
if (r - l + 1 >= k) lt.modify(0, (ll)k * v, l, r - k + 1);
lt.modify(-v, ll(r + 1) * v, std::max(l, r - k + 1), r);
if (r - k + 1 <= l) lt.modify(0, ll(r - l + 1) * v, r - k + 1, l);
}
}
for (int i = 0; i + k - 1 < n; ++i) std::cout << lt.query(i) << " ";
std::cout << "\n";
}
};
void SNOWFLAKE(int c, char* v[], int i) { delete new class SNOWFLAKE(c, v, i); }