题意
某大公司有这么一个规定:只要有一个员工过生日,当天所有员工全部放假一天。但在其余时候,所有员工都没有假期,必须正常上班。这个公司需要雇用多少员工,才能让公司一年内所有员工的总工作时间期望值最大(假设一年有 365 天,每个员工的生日都概率均等地分布在这 365 天里)?
题解
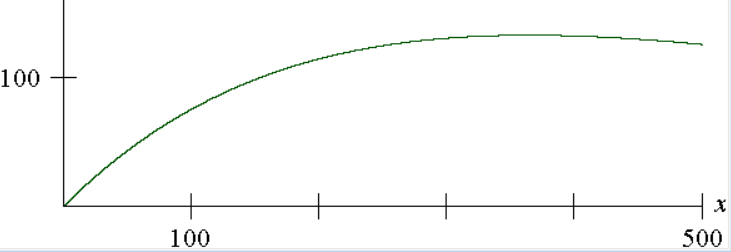
你的感觉或许是,50 人或 100 人左右吧。但其实答案是 365 人。
假设你雇佣了 $x$ 人。
在一天里,期望的工作时间为 $f\left(x\right) = \displaystyle x \cdot \left(\frac{364}{365}\right)^x$。考虑这个函数何时取到最大值。
我们来看一下 $\displaystyle \frac{f\left(x + 1\right)}{f\left(x\right)}$ 的值,它等于 $\displaystyle\frac{364\left(x+1\right)}{365x}$
显然,要到 x > 365 时,函数才是递减的。