题意
一个人(叫做小明)和一只鳄鱼同被关在一个半径为 $10$ 米的岛上,鳄鱼位于岛中心处,小明则在距离中心 $1$ 米的地方。两者的最大运动速度都是每秒 $1$ 米。鳄鱼有没有什么必胜策略,使得不管小明怎么跑,它总能在有限的时间里抓住小明?
(别问我鳄鱼为什么不能跳到水里,因为这是题目设定)
题解
我猜如果你想出来的话,应该想的是:
鳄鱼只需要始终保持自己与小明在圆盘的同一半径上即可。直觉上看,由于鳄鱼总是处在“内圈”上,因而不管小明跑到了哪里,鳄鱼总能轻松地与小明继续保持在同一半径上;并且,鳄鱼总有足够的余力向小明靠近,严格减小它与小明之间的距离,除非小明是沿着半径方向径直向外跑。由于岛的大小是有限的,小明不可能无限地向外跑,因而鳄鱼最终总会追上小明。
但是,后来人们发现,这个解法其实是错误的,原因很简单:能不断靠近小明,不一定就能在有限的时间里抓住小明,正如 1/2 + 1/4 + 1/8 + 1/16 + … 永远不会超过 1 一样。
查看正确做法
最终, A. S. Besicovitch 为小明构造出了一个极其巧妙的策略,使得鳄鱼无论如何都抓不到小明,从而完美地解决了这个问题。
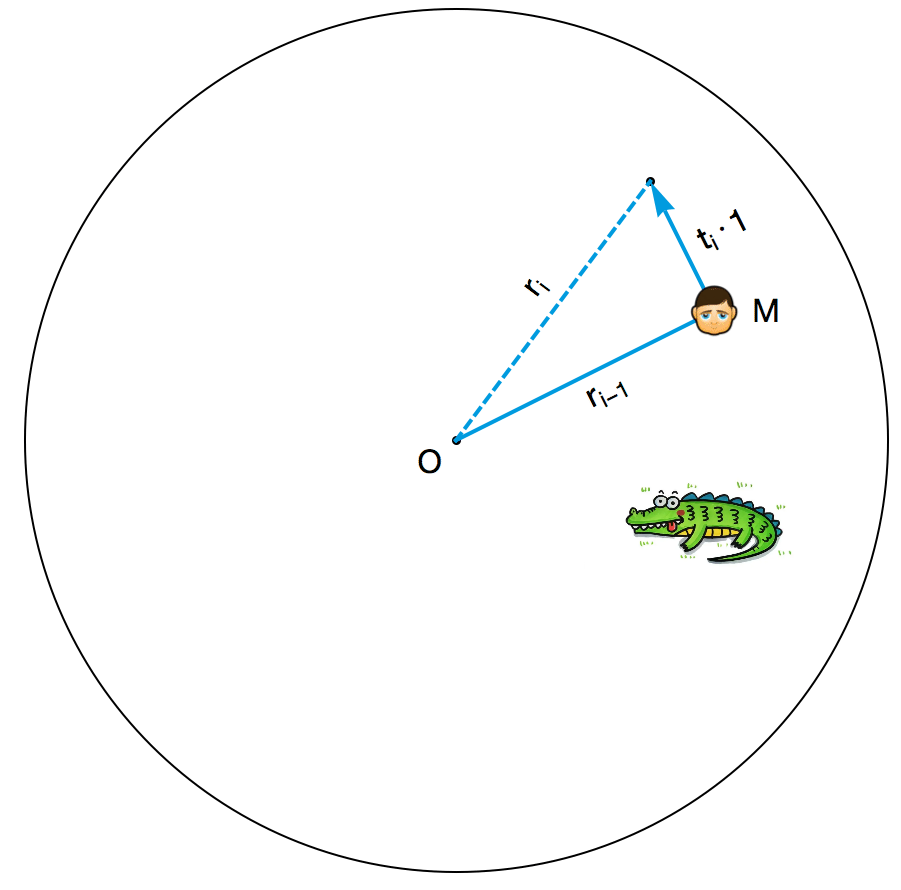
A. S. Besicovitch 为小明设计的策略如下。游戏开始后,小明首先把接下来的时间分成一小段一小段的,这些时间段的长度依次为 t1, t2, t3, t4, … 。不妨把岛的圆心记作 O ,把小明当前的位置记作 M 。每个时间段开始的时候,小明都会看看此时此刻线段 OM 的位置,并且沿着垂直于 OM 的方向,以最高速度往没有鳄鱼的那一侧跑去(如果鳄鱼的位置恰好位于 OM 所在直线上,则向任意一侧跑去)。容易看出,不管在哪个时间段里,鳄鱼都不可能追到小明。如果把第 i 个时段结束后小明与圆心的距离 OM 记作 ri ,那么由勾股定理可知:
${r_i}^2 = {r_{i-1}}^2 + \left(t_i \cdot 1\right)^2 = {r_{i-1}}^2 + {t_i}^2$
其中 $r_0 = 1$。
因此,当 $t_1 + t_2 + t_3 + \ldots + t_n$ 这么多的时间过去以后,小明与圆心的距离 OM 满足
$$OM^2 = {r_n}2 = 1^2 + {t_1}^2 + {t_2}^2 + {t_3}^2 + \ldots + {t_n}^2$$
最巧妙的地方来了。令 $t_i = \frac1i$,那么 $t_1 + t_2 + t_3 + \ldots$ 是发散的,但 ${t_1}^2 + {t_2}^2 + {t_3}^2 + \ldots$ 却是收敛的。
因而 OM$^2$ 始终不超过 $1 + 2 = 3$,OM 的长度也就始终不超过 $\sqrt3$,这远远小于竞技场的半径(事实上,OM$^2$ 的极限是 $\displaystyle1 + \frac{π^2}6$)。这说明,不管时间过去了多久,小明始终在坚持运动,并且运动路线始终在可活动范围以内。既然每一个时间段里鳄鱼都无法抓到小明,鳄鱼自然也就永远抓不到小明了。
参考
https://www.matrix67.com/blog/archives/6090