题意
注意,所有的 $h_{i, j}$ 都不会重复
稍微提高点难度吧,询问次数限制改为 $5n$。
题解
首先有一个一定能找到相对高地的方法(此处取名“蛇形法”,至于为什么,往下看就知道了):
随机一个点,寻问四周,向最高的点移动,直到四周都比它低。
<此处应有 $30$ 秒思考,你需要知道它为什么是对的,又需要知道它在什么情况下会超出询问次数>
查看答案
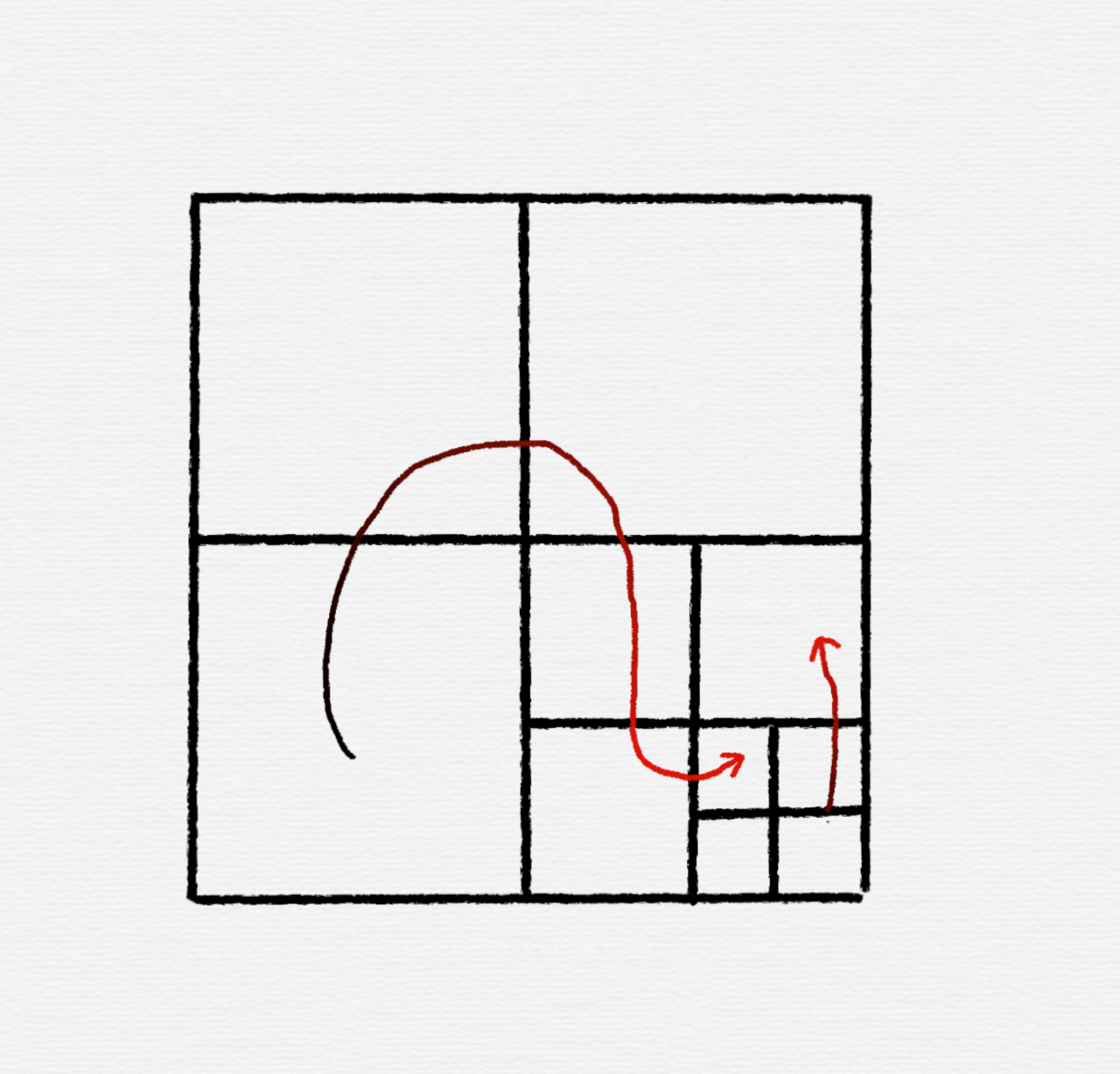
考虑一下这个 $5n$ 是怎么出来的。大概就是个分治。于是每次把 $n \times n$ 的大矩阵切成四个 $\dfrac n2 \times \dfrac n2$ 的小矩阵。我们的任务是通过几次询问操作来确定那个 $\dfrac14$ 小矩阵一定有相对高地。
首先,显然想到的是询问一个“十”字框: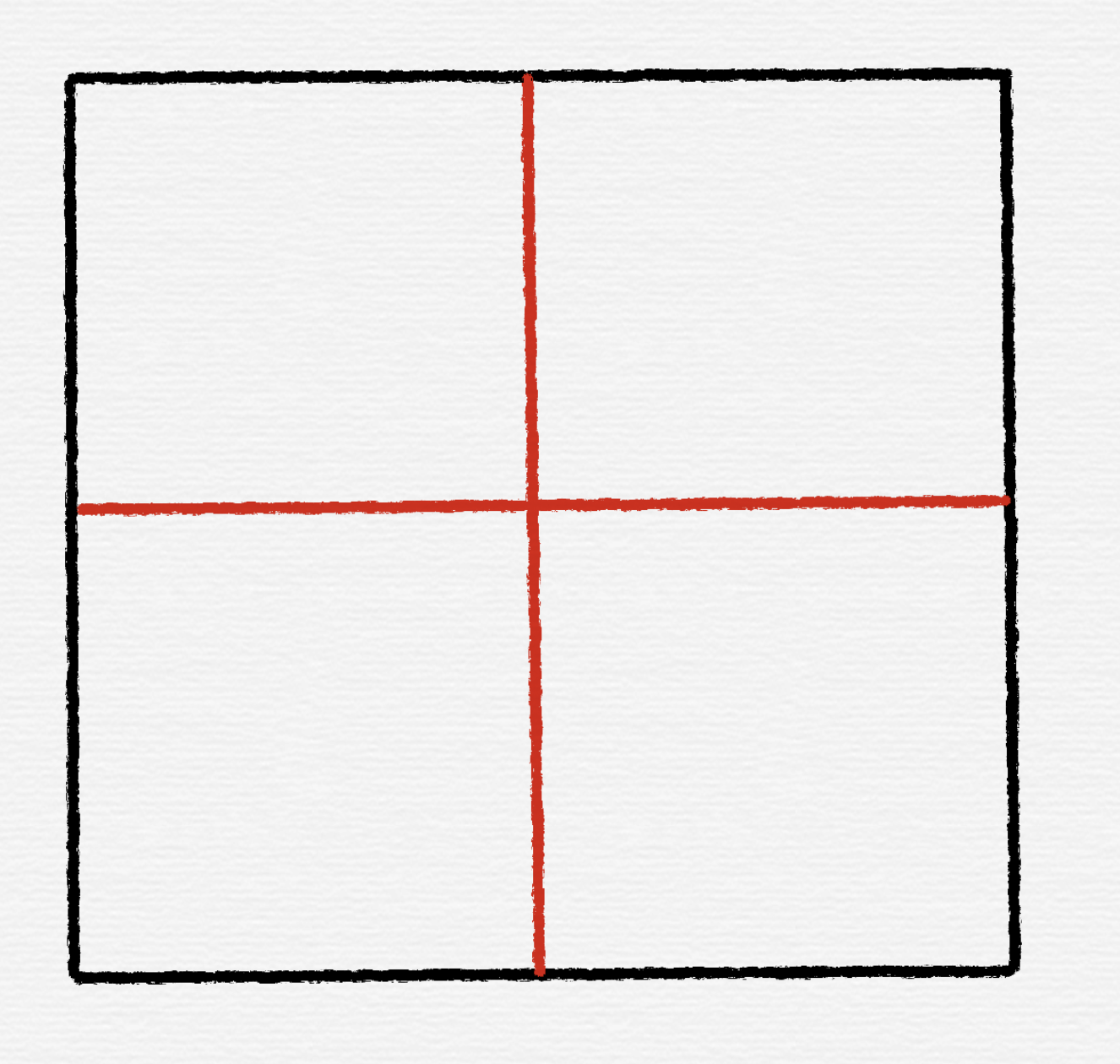
然后找到框上最大的一个点,看它剩下的两个方向(有两个方向在框上,已经确定比它低了)的高度,如果都比它低,此点既是相对高地。否则,高的一边所在的 $\dfrac14$ 小矩阵一定有相对高地(此时回想一下之前那个“蛇形法”,你应该就能理解这个为什么是对的了)。
现在告诉你,目前为止是对的,但如果继续用这个方法找答案就不对了。
<此处应有较长时间的思考,你需要知道它为什么第二次走的时候就有可能出错了,这是此题的关键之一>
查看答案
想出来了?没想出来建议你再想一想。展开答案
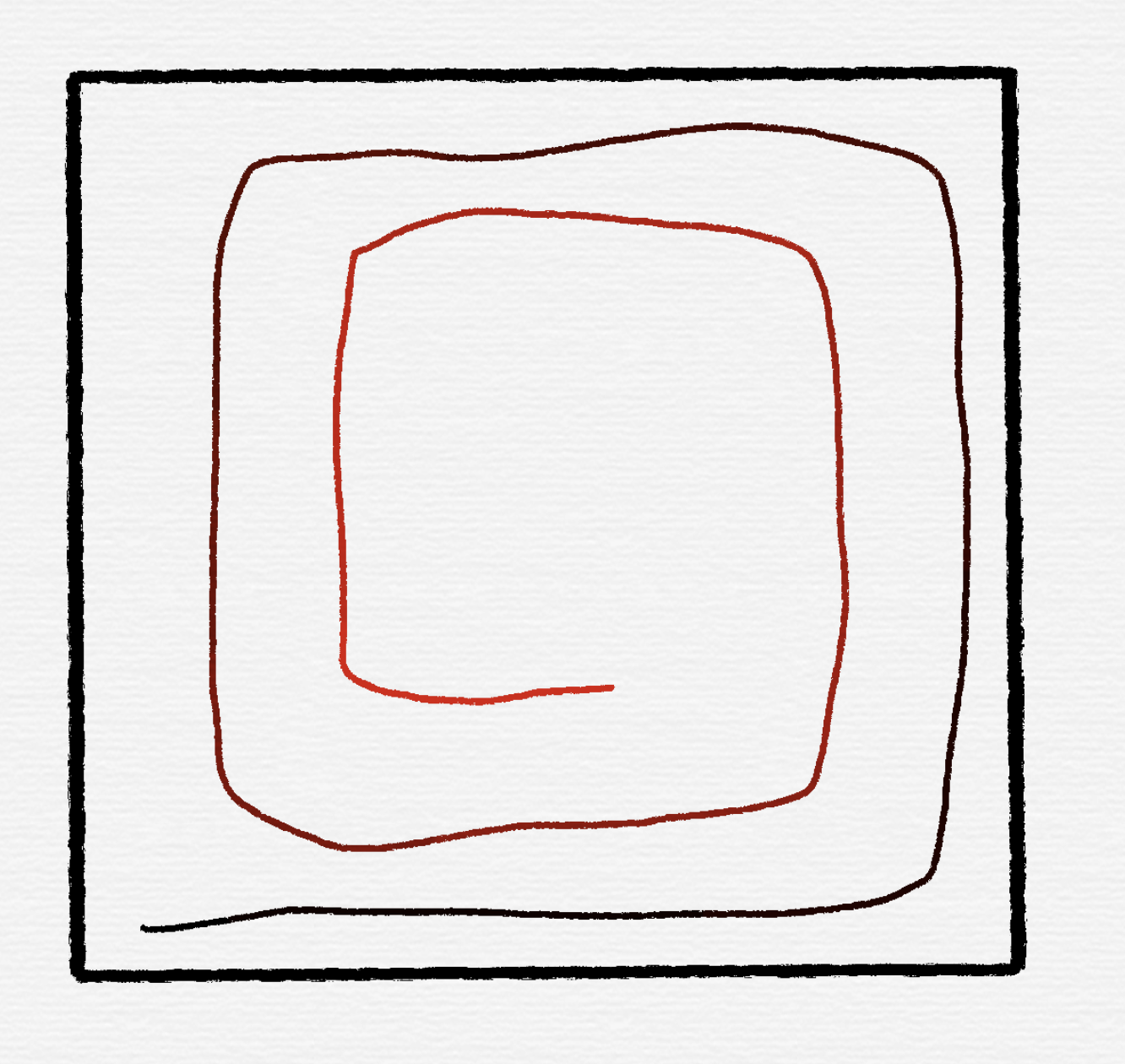
越红代表越高。请模拟一边算法流程,如果你不懂,建议停下思考或重新阅读本文。
<此处应有 $30$ 秒思考,你需要想想如何解决这个问题>
解决方法
询问“田”字而不是“十”字。
询问复杂度分析
第一次只需要询问一个“十”字,复杂度为 $\mathcal O\left(2n\right)$。
下一次:询问一个“田”字,其中有一半会在第一次寻问的“十”字上,于是只有中心十字的 $\mathcal O\left(n\right)$ 和外层“田”字的一半 $\mathcal O\left(n\right)$ 需要询问。
第三次:“田”字已经在前两次操作时都询问完了,因此只有中心十字的 $\mathcal O\left(\dfrac n2\right)$ 需要询问。
之后每次的询问次数都是上次的次数除以二,因此总询问次数为:
$$\mathcal O\left(2n + n + n + \frac n2 + \frac n4 + \frac n8 + \cdots\right) = \mathcal O\left(5n\right)$$
稍微卡卡常即可。
$4n$ 做法
我们需要从本质上考虑“十”字法为什么会错。
<此处应有 $10$ 秒思考>
就是因为上次找到的相对高地的线被跟丢了。因此只要把上次“十”字考虑进来就行了,不需要任何额外询问。
$$\mathcal O\left(2n + n + \frac n2 + \frac n4 + \cdots\right) = \mathcal O\left(4n\right)$$