题目
题解
T1
我们可以把问题看成：
有 $n$ 个人，$k$ 个水龙头，第 $i$ 个人需要打 $d_i$ 时间的水，求最少时间。
这个的思路很简单，每次我们让一个人去使用时间最少的水龙头，开个堆就行了。如图
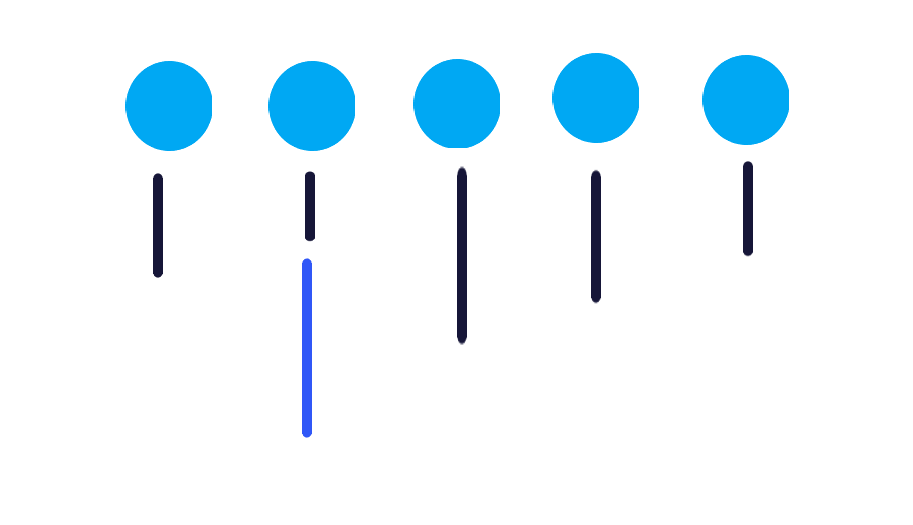
蓝色的点表示水龙头，黑色线段表示已经安排好的人，蓝色线段表示现在正在分配的人。
这样，我们只要二分 $k$ 即可。时间复杂度 $\mathcal O\left(n \log n\right)$。
T2
送分题，因为 Bessie 只能变一次手势，所以我们枚举分界点。做前缀和与后缀和，时间复杂度 $\mathcal O\left(n\right)$。
T3
我们把串长度补到 $2$ 的整数次幂，设补完后的串为 $s$。如果 $n$ 在 $s$ 的左边（$n \leq s$ 长度的一半），就在左边寻找；否则，在右边找到对应到左边的位置，然后在左边查找。时间复杂度 $\mathcal O\left(\log n\right)$。