机器学习 分类问题

概述

本文将讲述基础的机器学习理论。从零开始，推导一个机器学习模型。

目的

我们的目的很简单，做出一个能识别手写数字的模型。为了简单起见，本文只讨论如何让模型区分两个数字，即输入手写图片，让模型判断是 $3$ 还是 $7$。

表示方式

为了配合 MNIST 训练集，我们统一使用 $28 \times 28$ 大小的 8-bit 灰度图片，来表示手写数字的图像。每个像素应该是一个 $0$ 到 $255$ 的数，表示灰度。

大体思路

很简单，我们对于每个像素 $a_{i, j}$，附上一个权重 $w_{i, j}$，最后算 $\sum w_{i, j} \cdot a_{i, j}$ 是否大于我们的阈值 $b$ 即可。

训练的方式如下：

• 如果正确，则什么也不做
• 若果错误，适当调整每个 $w_{i, j}$ 和 $b$ 的值

机器学习的关键在于如何调整 $w_{i, j}$ 和 $b$，下文会详细表述。

我们看看这个东西有没有理论依据，这个东西有戏吗？

实际上，对于特征点（比如 $3$ 中间位置的凸起）所在位置拉高权重，对于相似点拉低权重（比如 $3$ 上方接近“横”的那部分，和 $7$ 就高度重合），即可识别了。这点与人类识别的方式也比较相似。

从更本质的角度分析，我们可以对比人脑的神经元。

每个神经元接受来自其他神经元的树突信号，可能是刺激信号，或者抑制信号。而每个神经元的状态只有激活和未激活两种。但是每个上游信号的权重不同。

人类的智慧足以验证我们这套理论的可行性。

一个例子

比如，在二维平面上有一些点，分为第一类点和第二类点，我们要让模型画一条直线，让这条直线左边只有某一类点，另外一边只有另外一种点。

首先想想我们的直线如何表达。我们用 $w_1x_1 + w_2x_2 = b$ 当分割线即可。

机器学习的关键就在于如何让机器自己去调这个 $w_i$。在机器开始调整之前，我们得先让机器知道自己对了还是错了。机器自己当然没法确认，还得是我们给出答案，让机器去核对。设正确答案是 $Y$，机器给出的答案是 $y$，如果 $Y \neq y$，说明机器错了。我们设每个 $w_i$ 的改动量为 $\Delta w_i$，很明显，改动肯定要跟输入有关。怎么算 $\Delta w_i$ 呢？关键是让机器知道 $w_i$ 是大了还是小了。我们发现 $Y - y$ 刚好可以满足我们这个要求。如果 $Y - y > 0$，说明我们要提高 $w_i$，让 $w_ix_i > b$，反之亦然。我们还需要评估 $x_i$ 带来的影响。显然 $x_i$ 越大，对整个函数的影响也越大，$w_i$ 响应的要提升更多。于是我们的调整公式也出来了：

$$\Delta w_i = \left(Y - y\right)x_i$$

问题来了，$b$ 要不要动？其实我们可以加个小动作，比如 $b = \left(Y - y\right)$，这样做其实是有意义的。

这样未免也太过死板了，完全根据输入调整真的可以吗？在真实的机器学习过程中，我们可能会再乘上一个常数 $r$，代表学习率，我们以后再讲。

一个问题

早在 1957 年，Frank Rosenblatt 就发明了这种感知器。但这种模型有个致命的缺陷：很多数据根本无法用一条直线（或者超平面）完成分类。比如：

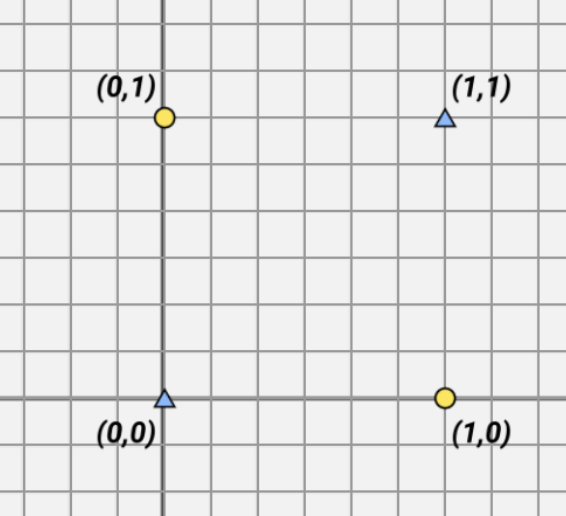
不可能用直线分开。

处理这个问题的方法也很粗暴，把空间扭曲：

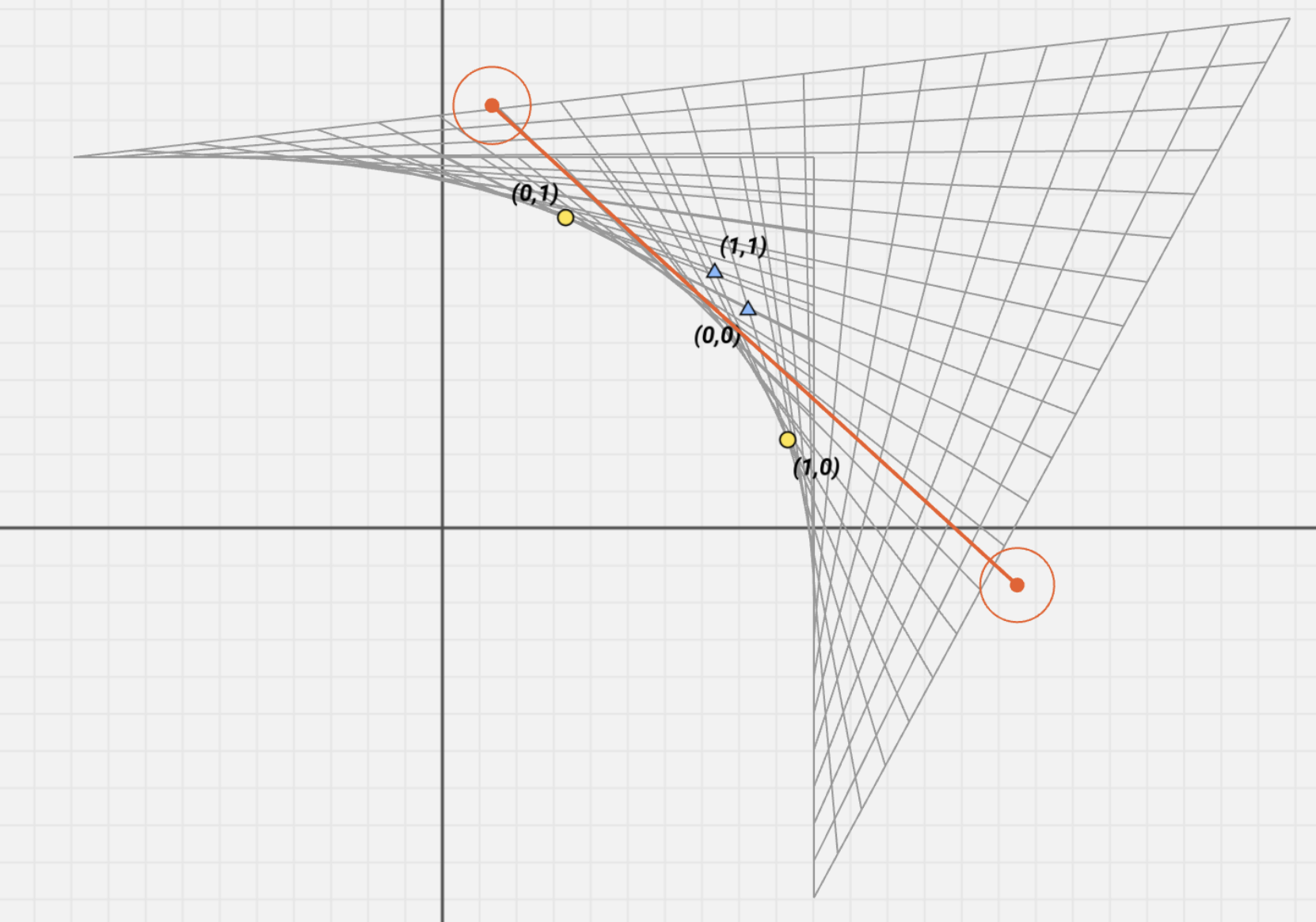
为了做到这点，我们不能再做简单的线性变换了，必须得加一个非线性的东西，让这个函数不再线性。其实这个就是激活函数。我们刚才用的是阈值门，大于 $b$ 就激活，否则就不激活。有关其他激活函数的东西我们以后再讲。

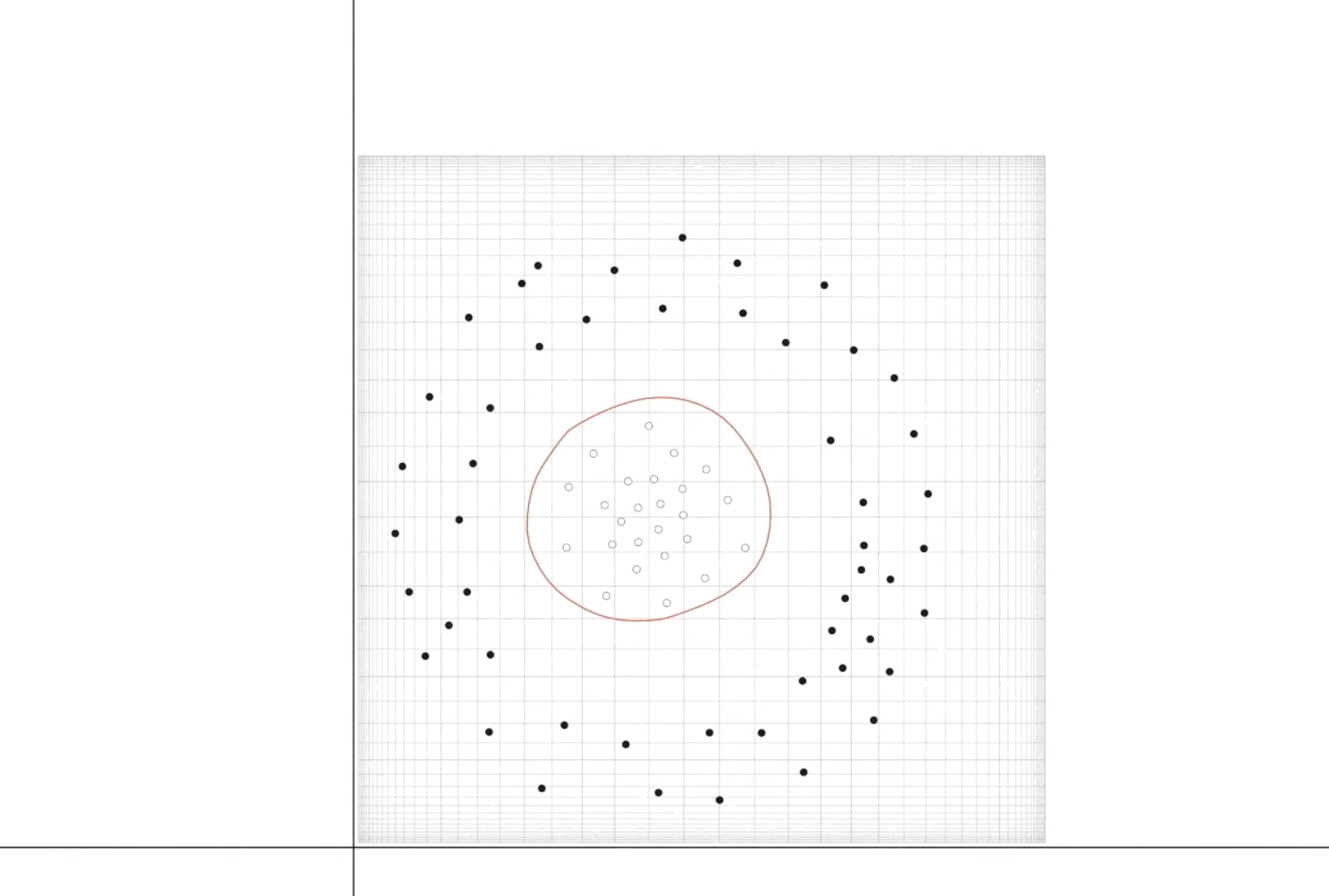
但是，这样就行了吗？我们可以举一个反例：在二维空间里，把内圈和外圈通过直线分开。无论是什么激活函数，都难以做到这一点。我们需要更牛逼的东西。

如果我们用三维呢？这相当于是把二维中原本密集的东西变换为三维中稀疏的东西，从而更好分类。我们来看看现在的神经元张啥样。

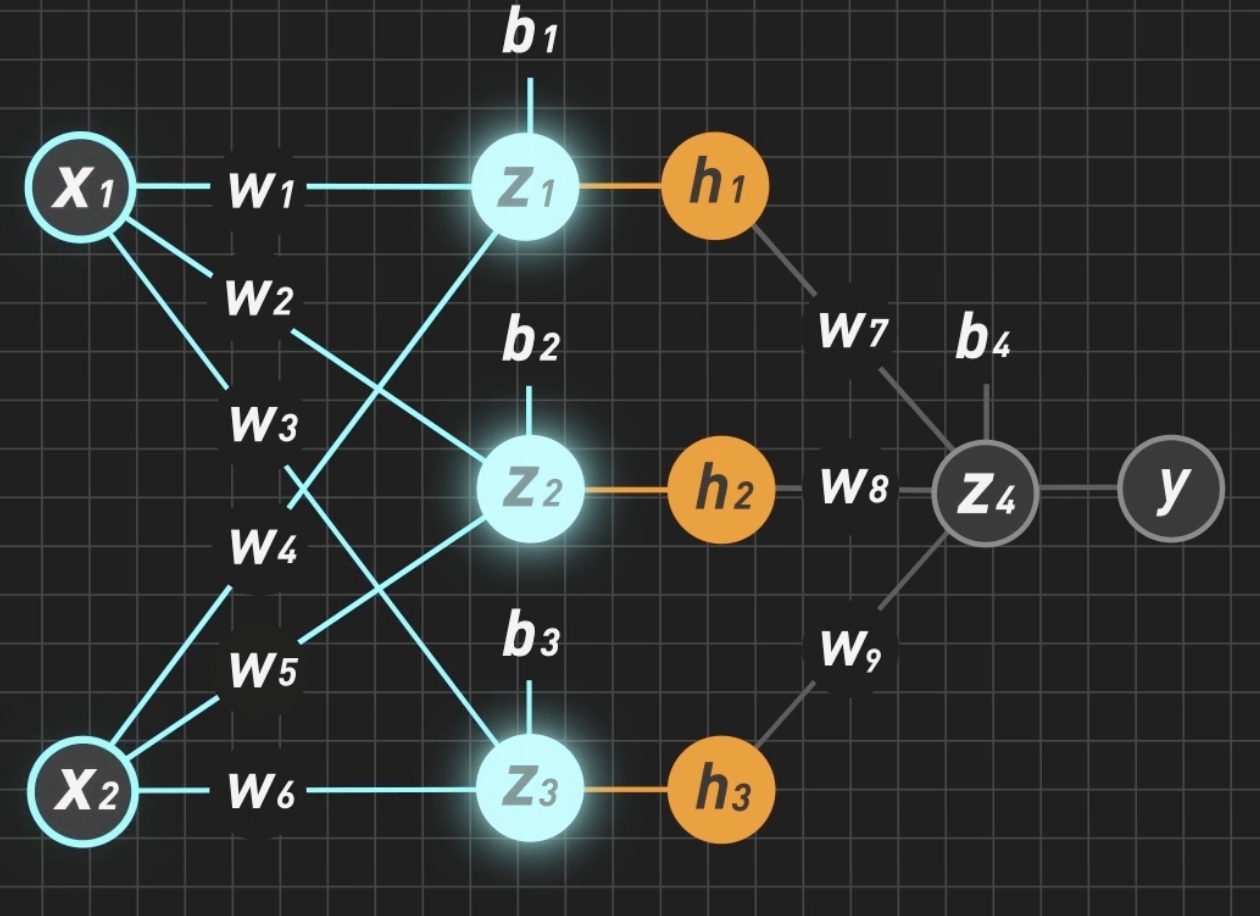
$z_i$ 就是我们三维空间中的坐标！$h_i$ 是我们的激活函数。

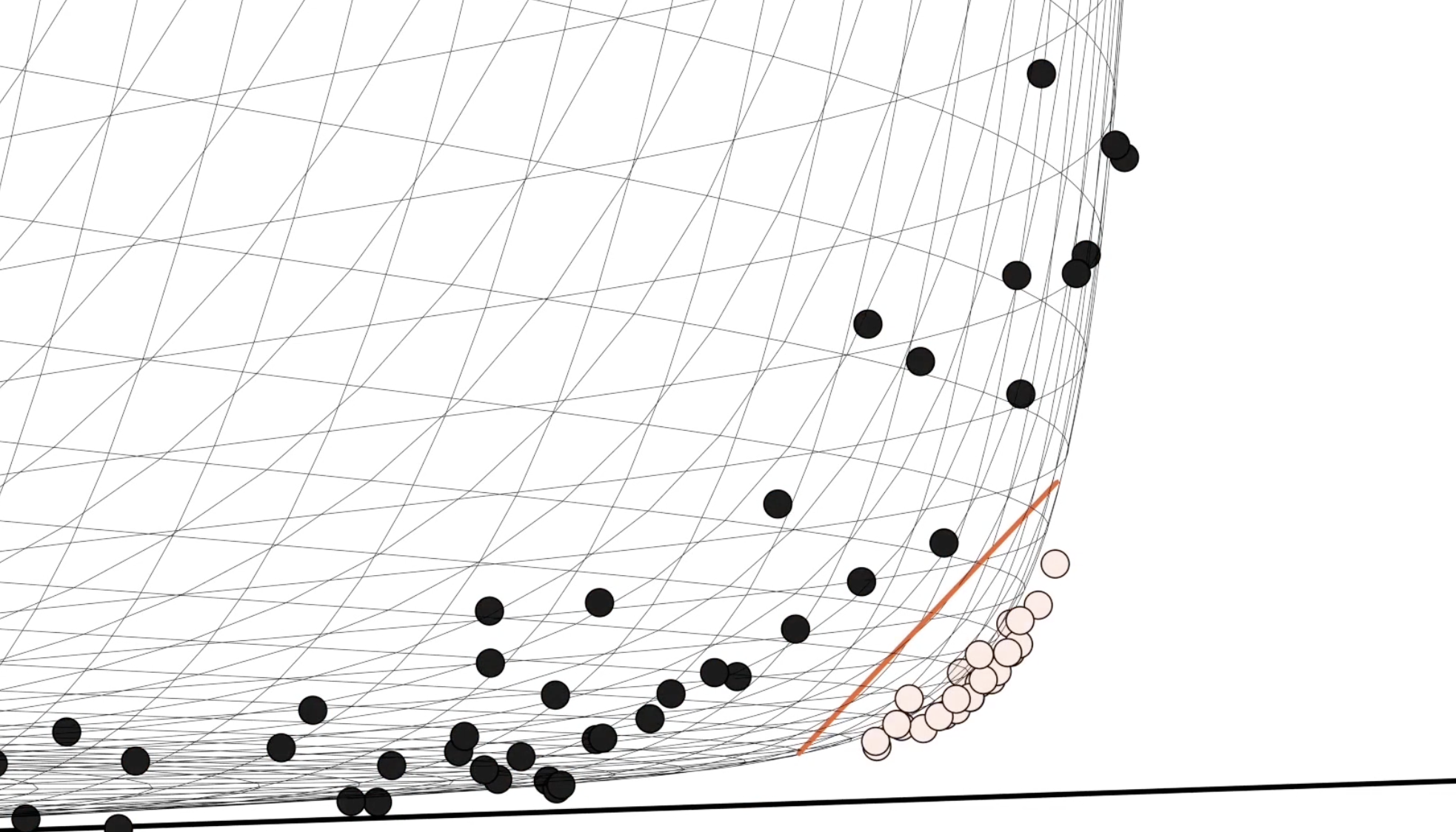
如果我们把这条线投影到二维平面上，会发现这条线变成了一个圆环！

损失函数

为了让机器知道什么好，什么不好，我们需要给每个状态做一个估价。这个函数，就是损失函数。比如，我们可以把损失定义为：

$$Loss\left(x_i\right) = \frac1n\sum\limits_{1 \leq i \leq n}\left\lvert Y_i - y_i\right\rvert^2$$

如此，机器就可以自动寻路，找到 $Loss$ 最小的那个点了。

具体方法是用梯度下降，之后我会发一篇新东西讲梯度下降。

施工中。。。

---

• Category: AI
• Last update: 2024-07-22 04:31:31^UTC+8
• Tags: No tags