前置知识
- 全微分
- 偏微分
- 积分
概述
拉格朗日乘数(Lagrange multiplier,又称 拉格朗日乘数法)用来解决 存在关系的多变量中的最值问题。
其实感觉在 OI 中使用得比较少。但是在数学填空题里或许可以发挥一些作用。还有可以在朋友面前装逼。
公式
众所周知,函数微分之后可以求出极值,但很多时候找到该函数的显式表达是很困难的,特别是当函数有先决条件或约束时。此时,拉格朗日乘数 可能可以比较快速地求解。
我们求函数 $f\left(x_1, \ldots, x_n\right)$ 在满足所有 $g_i\left(x_1, \ldots, x_n\right) = 0$ 的局部最值。
$$\mathcal L\left(x_1, \ldots, x_n, \lambda_1 \ldots \lambda_k\right) = f\left(x_1, \ldots, x_n\right) - \sum\limits_{i = 1}^k \lambda_ig_i\left(x_1, \ldots, x_n\right)$$
接下来对 $x_1, \ldots, x_n, \lambda_1 \ldots \lambda_k$ 都分别求偏微分,并且令每个导数都等于 $0$,满足条件的 $x_1, \ldots, x_n$ 都有可能成为最值(很抽象,看不懂很正常,看看例子就懂了)。
拉格朗日乘数法所得的临界点会包含原问题的所有临界点,但并不保证每个拉格朗日乘数法所得的临界点都是原问题的临界点。
原理
这不是证明。
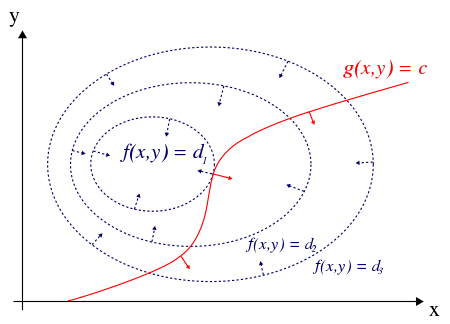
红线标出的是约束函数 $g\left(x, y\right) = c$ 的点的轨迹。蓝线是函数 $f$ 的等高线。箭头表示梯度,和等高线的法线平行。
它们相切的时候,就会出现极值。取偏微分等于 $0$ 的解即可求出。
例子
先看几个例子,再看证明。
一个二维的例子
求函数 $f\left(x, y\right) = x^2 + y^2$ 在满足 $g\left(x, y\right) = xy - 1 = 0$ 时的最值。
$$\mathcal L\left(x, y, \lambda\right) = x^2 + y^2 - \lambda\left(xy - 1\right)$$
- 对 $x$ 求偏微分:$2x + y\lambda = 0$
- 对 $y$ 求偏微分:$2y + x\lambda = 0$
- 对 $\lambda$ 求偏微分:$xy - 1 = 0$
满足上述条件的只有:
$$ \begin{cases} x = 1 \\ y = 1 \\ \lambda = 2 \end{cases} \; \begin{cases} x = -1 \\ y = -1 \\ \lambda = 2 \end{cases} $$
一个三维的例子
求函数 $f\left(x, y\right) = x^2y$ 在满足 $x^2 + y^2 = 1$ 时的最小值。
$\mathcal L\left(x, y, \lambda\right) = x^2y - \lambda\left(x^2 + y^2 - 1\right)$
将所有变量的偏微分设为 $0$,得到一个方程组,最值在以下方程组的解中:
$$ \begin{cases} 2xy + 2\lambda x = 0 \\ x^2 + 2\lambda y = 0 \\ x^2 + y^2 - 1 = 0 \end{cases} $$
证明
若函数 $f\left(x_1, \ldots, x_n\right)$ 在 $P$ 点处有极值 $v$,且在 $P$ 点的邻域内连续,则在 $P$ 处有:
$f\left(x_1, \ldots, x_n\right) = v$
另有一常值函数
$g\left(x_1, \ldots, x_n\right) = c$
两函数在 $P$ 点处的全微分为
$$\mathrm{d}f = \sum\limits_{i = 1}^n\frac{\partial f}{\partial x_i}\mathrm{d}x_i = 0$$
$$\mathrm{d}g = \sum\limits_{i = 1}^n\frac{\partial g}{\partial x_i}\mathrm{d}x_i = 0$$
$f\left(x_1, \ldots, x_n\right)$ 在区段内有极值的时候由于 $\mathrm{d}x_i$ 是任取的无穷小量,故该线性方程组的系数成比例,有
$$\dfrac{\dfrac{\partial f}{\partial x_i}}{\dfrac{\partial g}{\partial x_i}} = \lambda$$
即
$$\dfrac{\partial f}{\partial x_i} + \lambda \cdot \dfrac{\partial g}{\partial x_i} = 0$$
将上二式分别乘以 $\mathrm{d}x$ 和 $\mathrm{d}y$,再相加并积分,得到一新函数
$$\mathcal L\left(x_1, \ldots, x_n, \lambda_1 \ldots \lambda_k\right) = f\left(x_1, \ldots, x_n\right) - \sum\limits_{i = 1}^k \lambda_ig_i\left(x_1, \ldots, x_n\right)$$
那么,求原函数极值的问题就转化为求该函数极值的问题。
参考
https://ksmeow.moe/method_of_lagrange_multiplier/
https://www.luogu.com.cn/blog/s-r-f/oi-bi-ji-li-yong-la-ge-lang-ri-sheng-shuo-fa-qiu-han-shuo-di-zui-zhi
https://en.wikipedia.org/wiki/Lagrange_multiplier