题意
给定一张无向联通图,小 B 从某个点开始,每秒移动到一个相邻节点(不能不动)。小 A 每秒猜测小 B 所在的位置。若小 B 刚好在小 A 所猜的位置,小 A 就赢了。
问小 A 能否在有限步数内赢。如果可以,给出步数最小的构造方案。
$1 \leq n \leq 1000$
题解
首先考虑有环的情况。小 B 可以选择从环上一点开始,每次随机向左或向右移动。小 A 无法在有限步数内确保找到小 B。
因此,只有在树中,小 A 才可能赢。
接下来考虑链的情况。
假设,集合 $S$ 表示所有当前小 B 能站的点的集合。
考虑小 A 猜一个点 $x$ 之后会发生什么。
首先,从集合 $S$ 中删除 $x$,然后新的 $S$ 变为旧集合 $S$ 中所有点能到的点的集合(扩展 $1$ 步),也可以理解为 $S$ 中的点的邻域的并。
最终目标是让 $S$ 成为空集。
这里有一个通用做法:
下图中打钩的点为 $S$ 中的点。
初始时是这样的: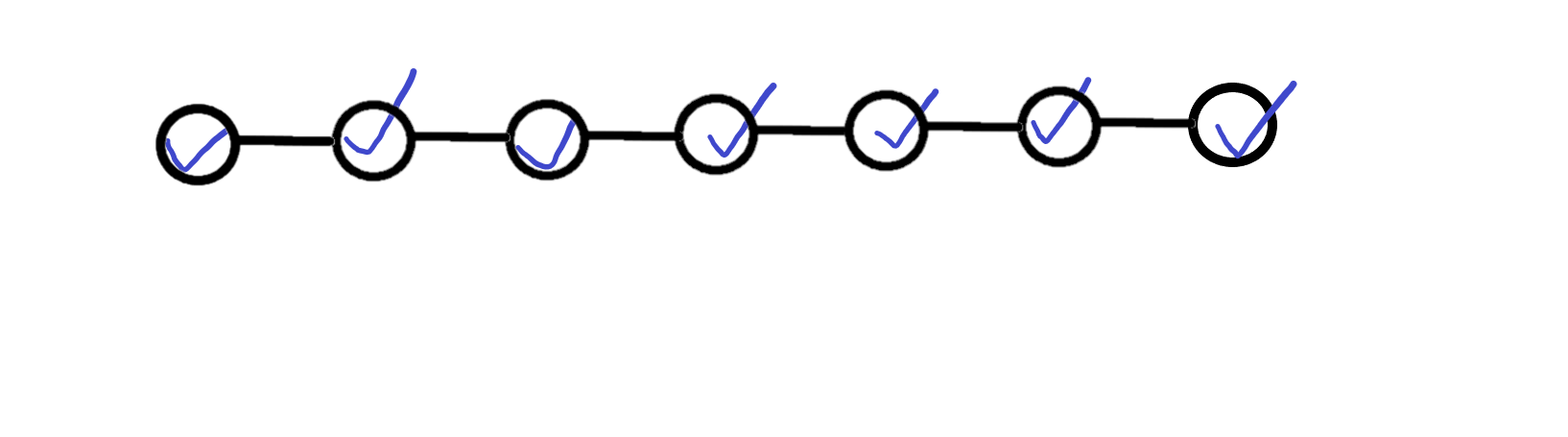
删去倒数第二个点,并扩展:
删去倒数第三个点,并扩展: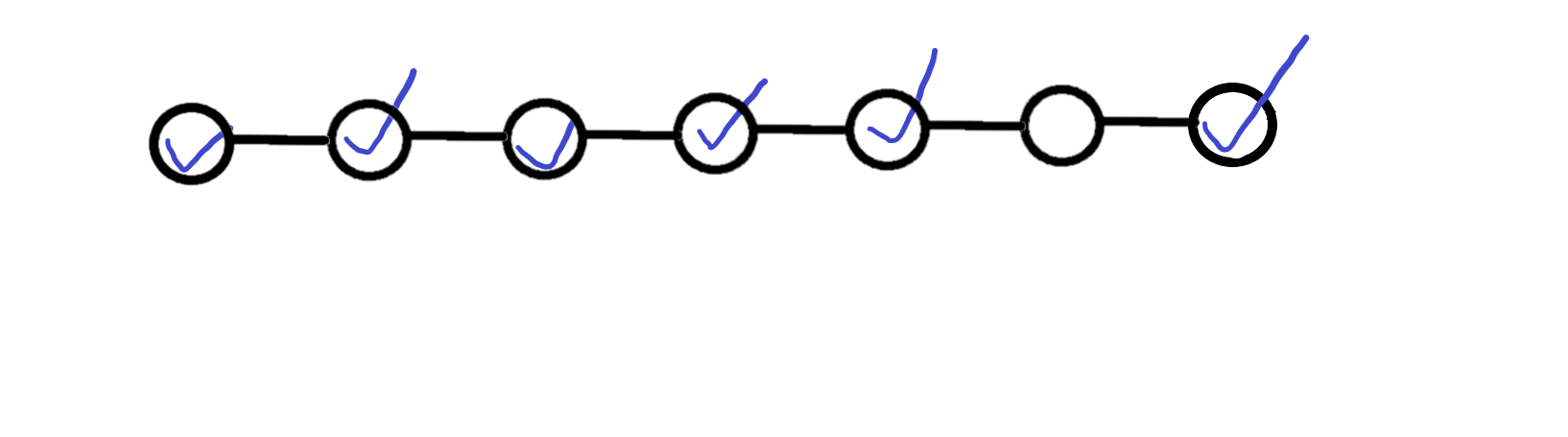
删去倒数第四个点,并扩展: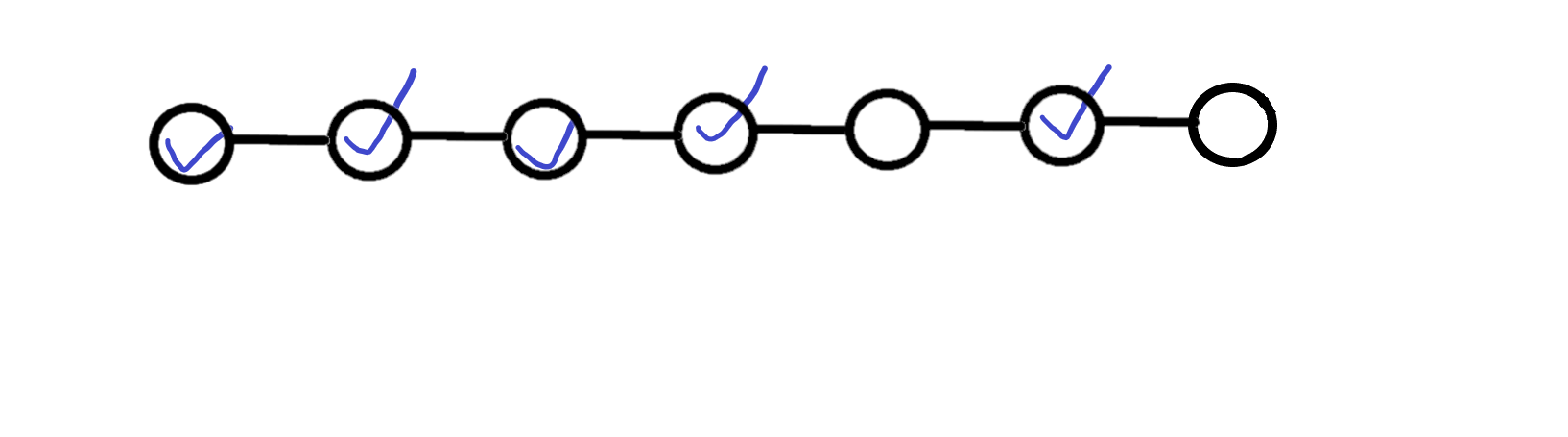
删去倒数第五个点,并扩展: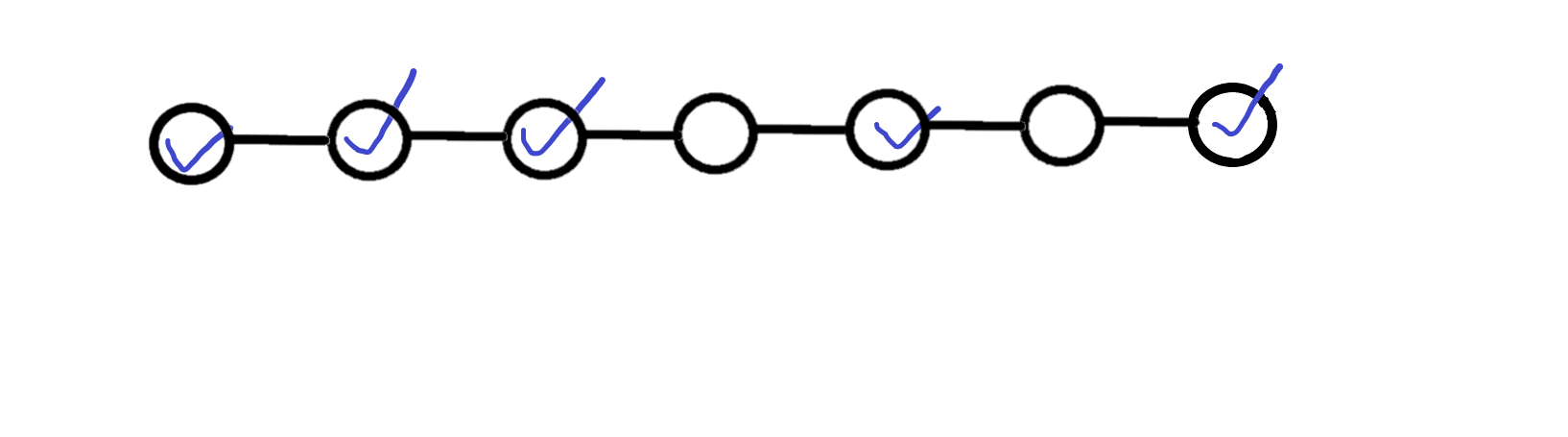
删去倒数第六个点,并扩展: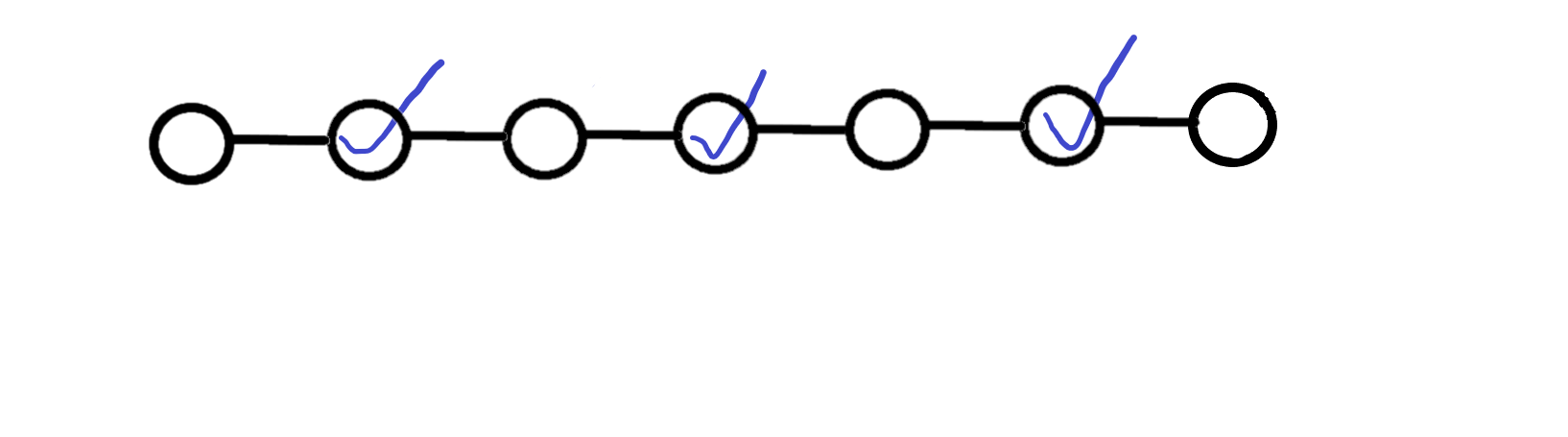
现在,这几个点不相邻了,不会互相影响。它们会在奇数点和偶数点中反复横跳,逐个删除即可。
在链中,小 A 必胜。
再看这样一颗树 $T$: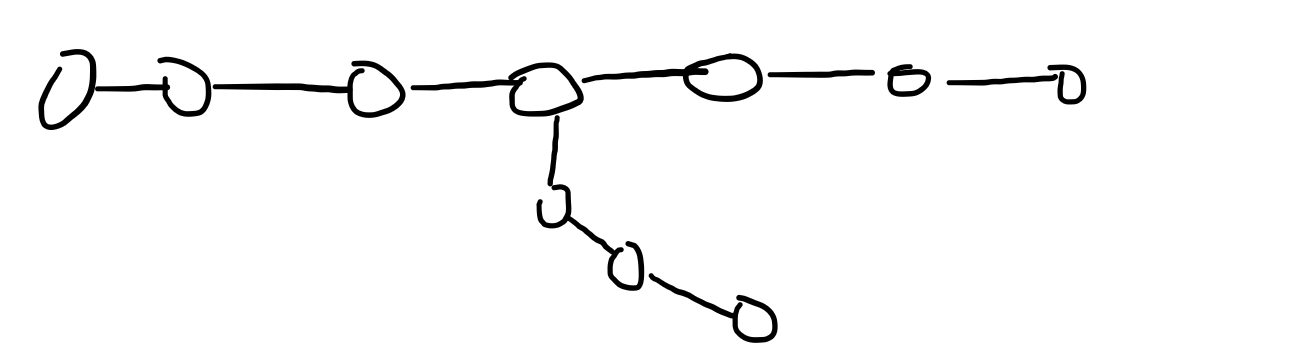
手玩一下会发现小 A 没有必胜策略。
这说明如果有点与链的距离达到或超过 $3$ 之后小 A 无法获胜。
考虑每个点与链的距离都不超过二(也就是不包含 $T$ 的树)。
以这个举例,框起来的是链上的点。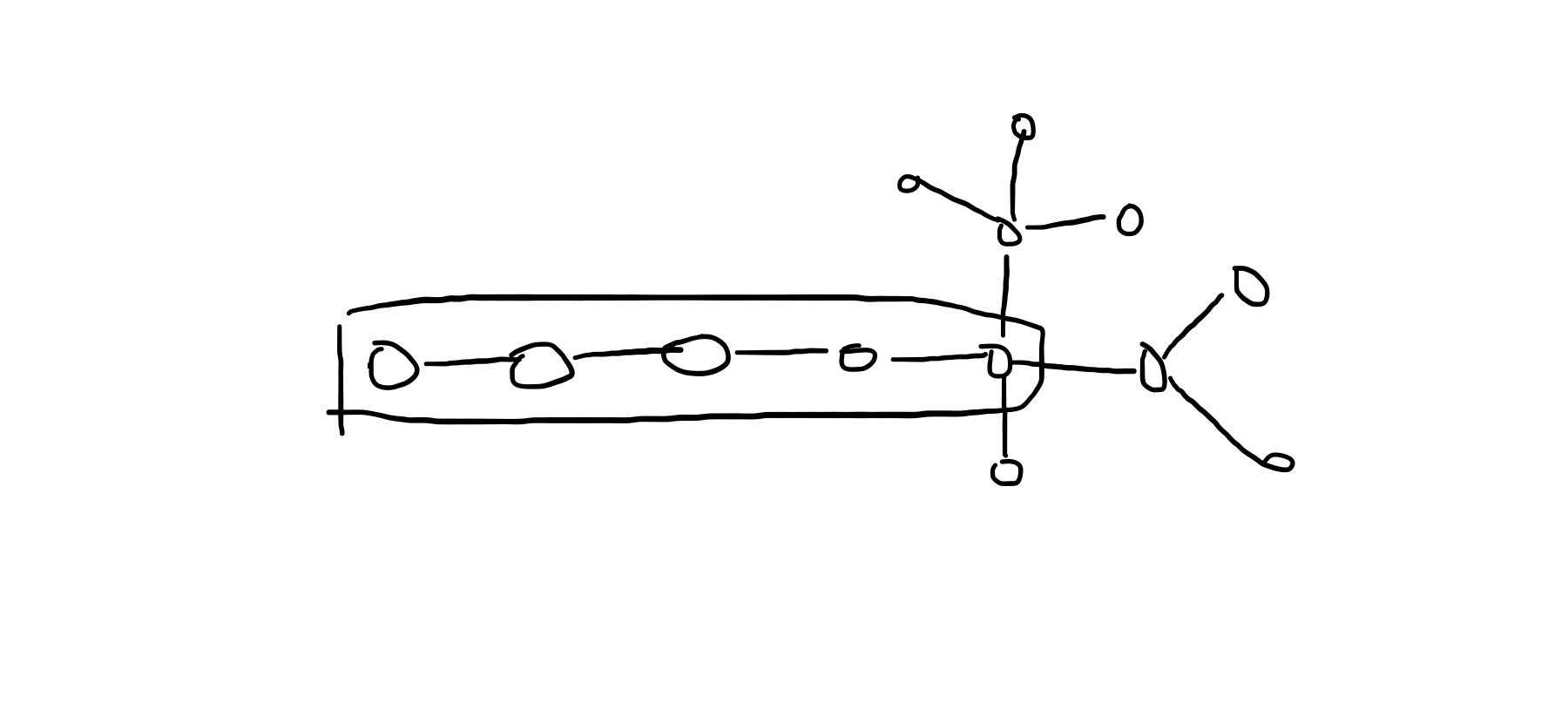
首先删打红叉的点,扩展: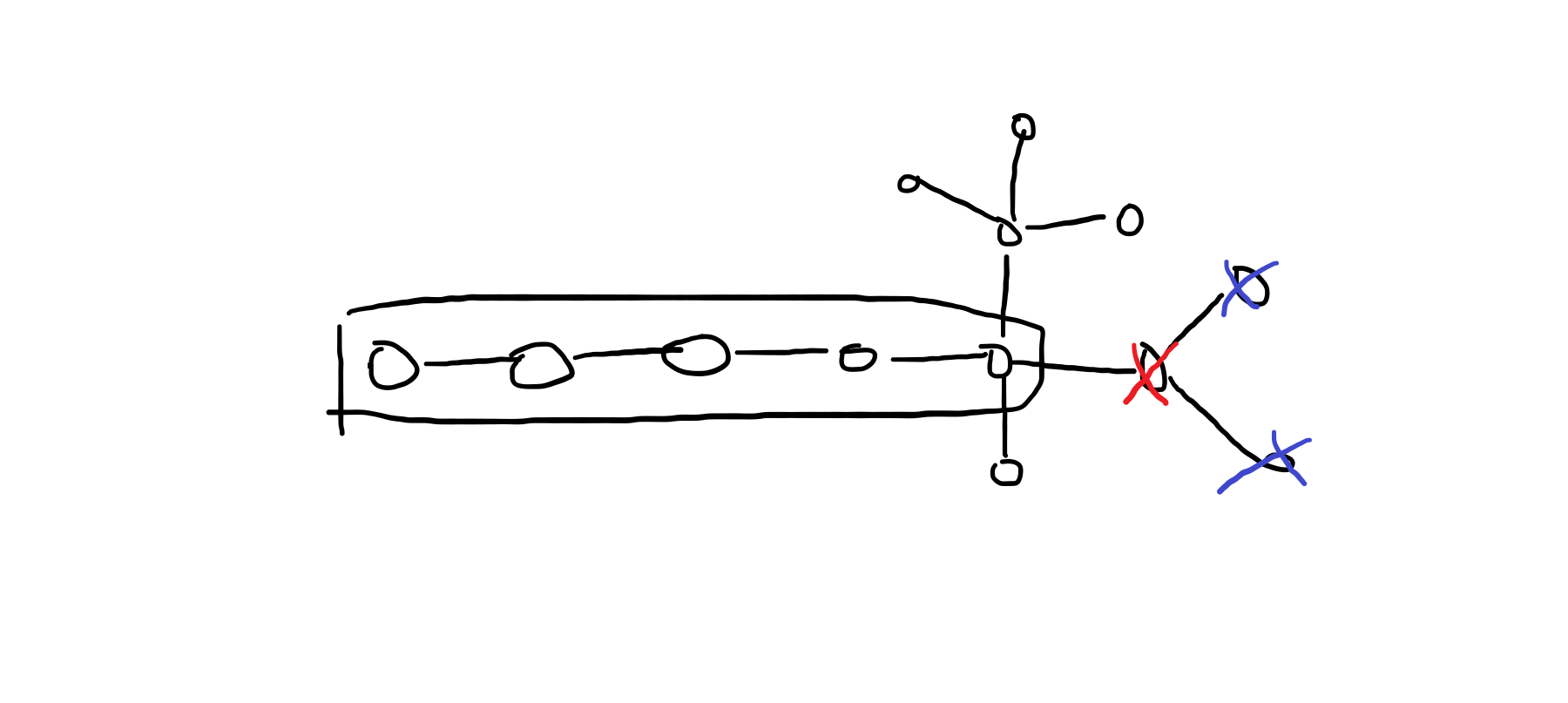
再删打红叉的点,扩展: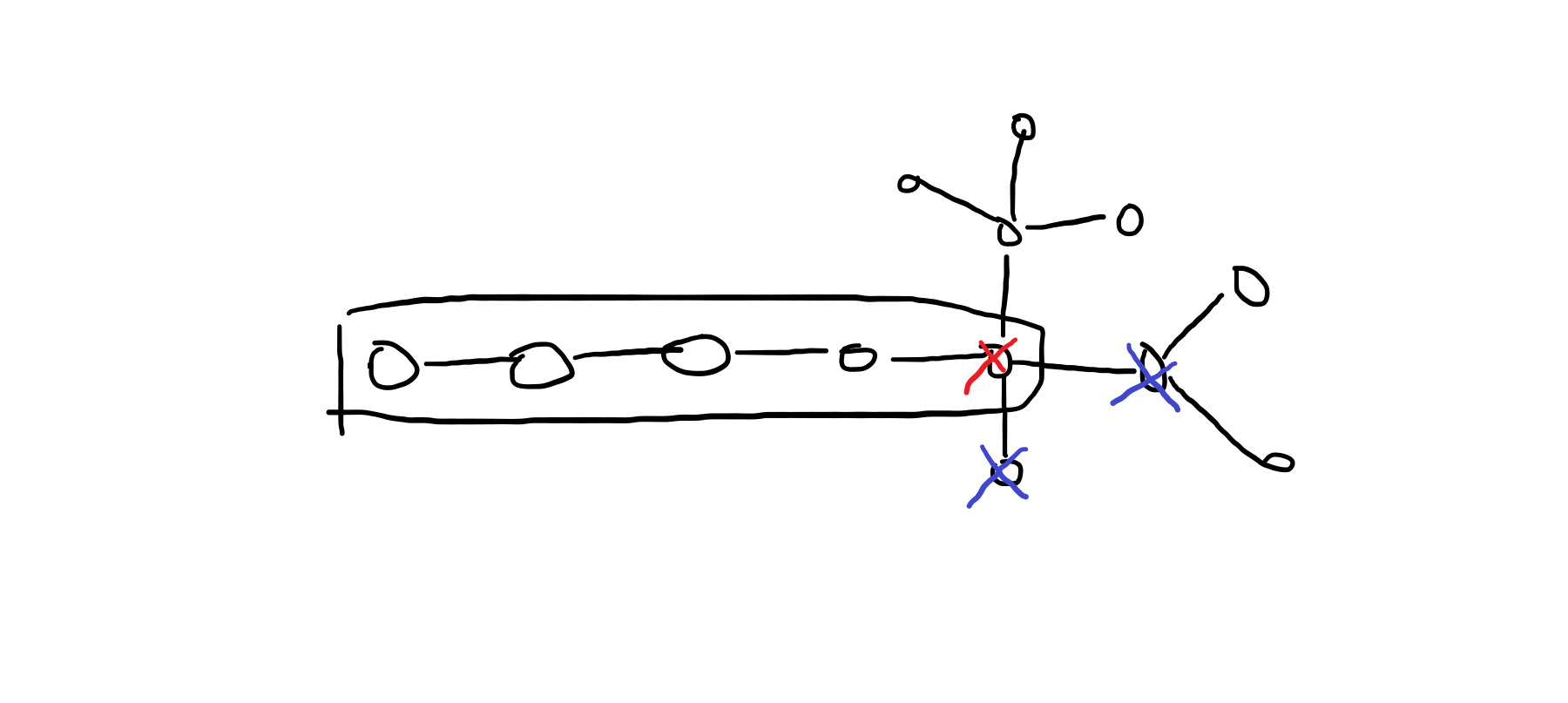
再删打红叉的点,扩展: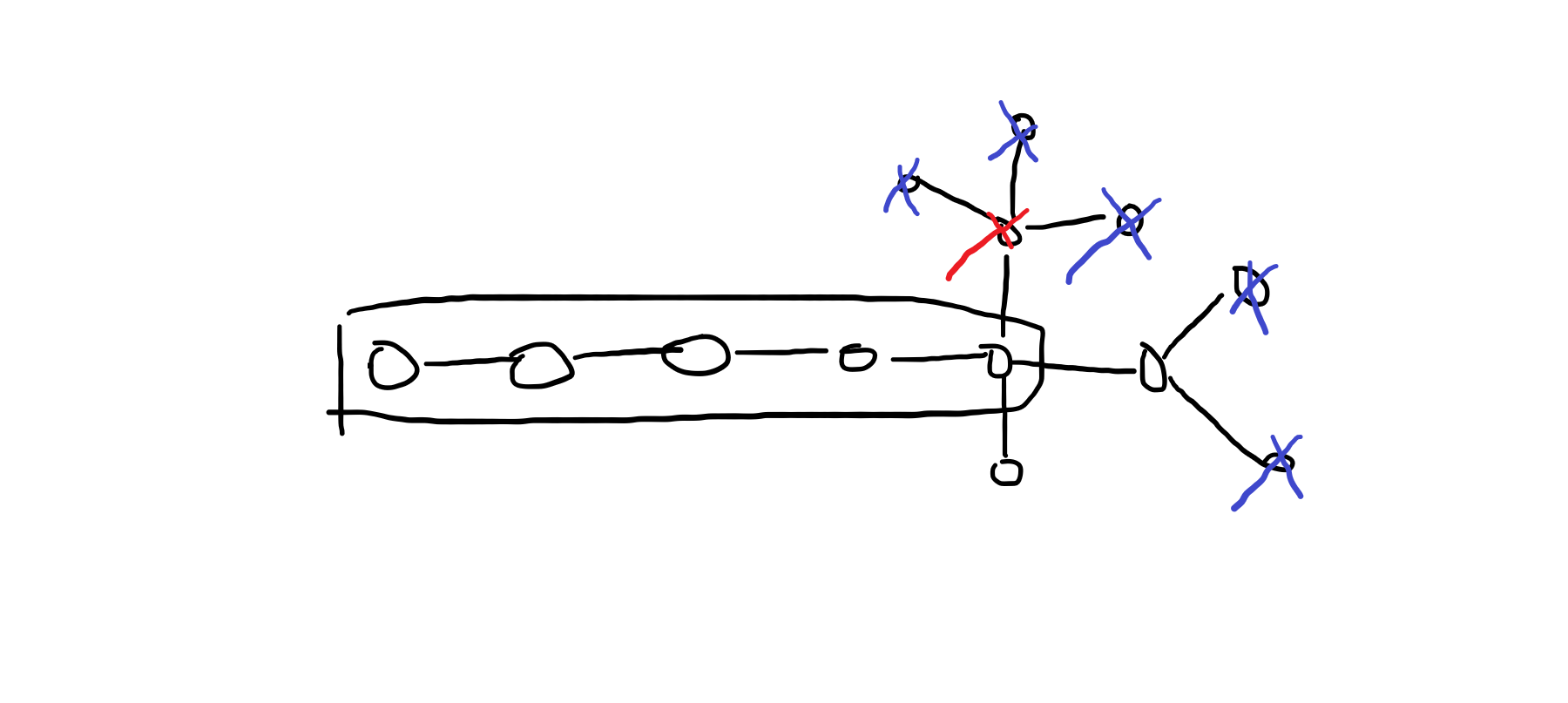
再删打红叉的点,扩展: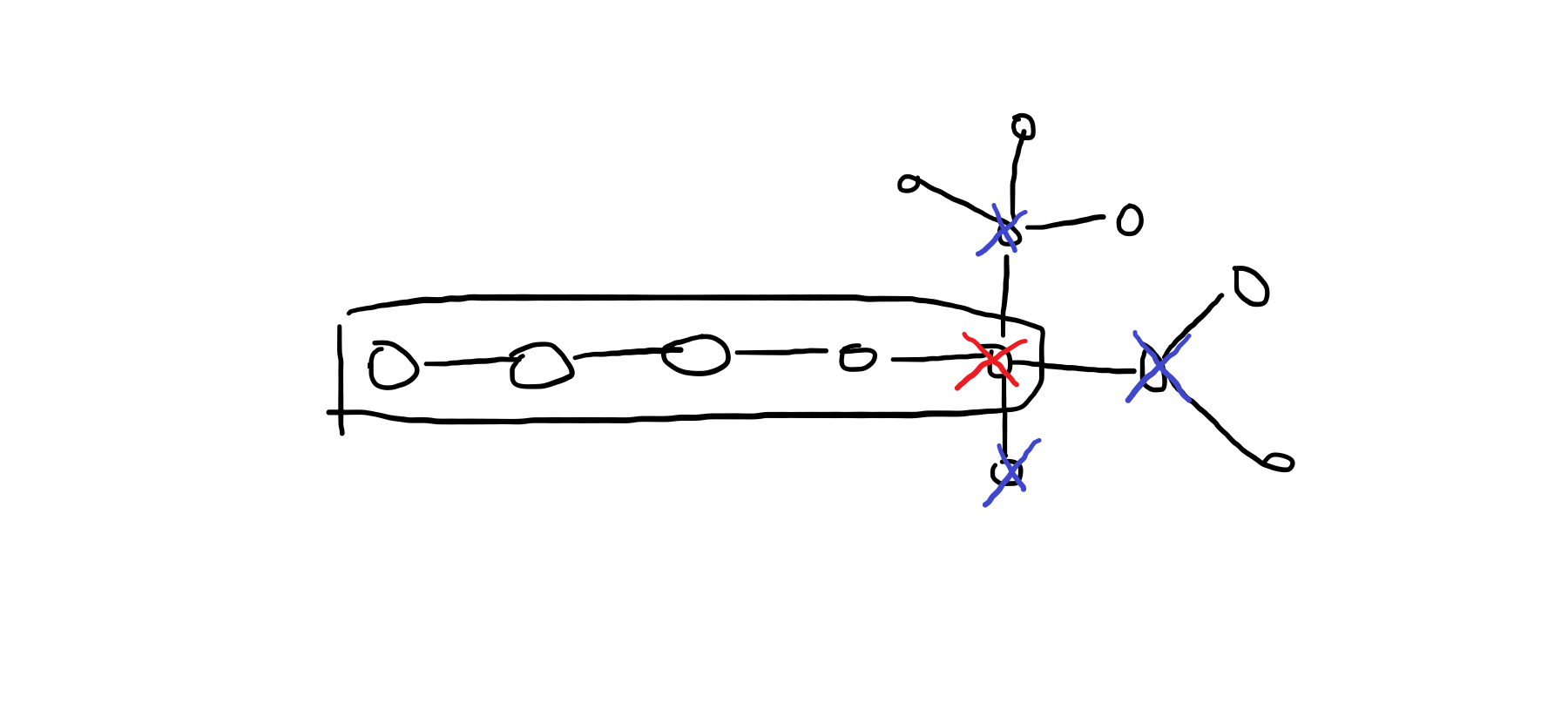
我们发现,链上最右边的点的任务已经完成了。这几个点不相邻了,不会互相影响。它们会反复横跳,逐个删除即可。
所以,在每个点与链的距离都不超过二的树上,小 A 无法获胜。
现在我们需要找到一个最优的方案。其实上述方法已经是最优的了。首先我们可以把点分为三类:链上节点、叶子节点和中间节点。
设 $z\left(x\right)$ 表示与 $x$ 相邻的中间节点的个数。
那么链上节点 $x$ 会被猜测 $2\left(z\left(x\right) - 1\right)$ 次。
叶子节点不会被猜测。
中间节点会被猜测 $2$ 次。
显然,如果中间节点次数减少,小 A 就无法通过上述方法抓住小 B 了。
如果 $v$ 是链上节点(以下证明来自官方题解):
设 $a$ 数组表示小 A 的猜测序列,设 $k = z\left(v\right)$。
小 B 将会再次尝试尽可能靠近结点 $v$ 。设 $u_1, u_2, \ldots, u_k$ 为 $v$ 所有相邻的结点,${u_i}'$ 为 $u_i$ 不是 $v$ 的相邻的点。
在减少次数的情况下,小 A 最多能猜测 $u$ 结点 $2k - 3$ 次,所以她最多在偶数轮猜测 $k - 2$ 次或奇数轮猜测 $k - 2$ 次。我们假定她在偶数轮猜测了 $k - 2$ 次,则我们让小 B 在所有 $a_i \neq v$ 的奇数轮停留在 $v$ 结点。
现在,我们关注一些 $a_i, a_{i + 2}, \ldots, a_{i + 2l}$ 且全部等于 $v$ ,但 $a_{i-2}, a_{i+2l+2} \neq v$ 的序列。
我们可以选择出与 $a_{i - 1}, a_{i + 1}, a_{i + 3}, \ldots, a_{i + 2l + 1}$ 不同的结点 $u_j$,因为 $l < k - 2$ 。故在所有奇数轮,小 B 移动到 ${u_j}'$ 。
我们现在知道了所有奇数轮时小 B 的位置。
而对偶数轮来说,我们认为小 B 在奇数轮所在位置的相邻结点。如果至少一回合他在 ${u_j}'$,他会在相应的偶数轮位于 $u_j$ 。如果在两个相邻的回合他都在 $v$ 结点,他可以简单地选择那个小 A 在偶数轮不会猜测的 $u_j$。
这也就意味着,我们无法减少猜测次数。因此,上述方案就是最优的。
代码
#include <bits/stdc++.h>
#define FOR(i, a, b) for (int i = (a); i < (b); i++)
#define REP(i, n) FOR(i, 0, n)
#define ll long long
using namespace std;
const int MAXN = 1010;
vector <int> ve[MAXN];
int bio[MAXN];
void impossible() {
cout << "NO\n";
exit(0);
}
void dfs(int x, int par) {
bio[x] = bio[par] + 1;
for (int y : ve[x]) {
if (y == par) continue;
if (bio[y]) impossible();
dfs(y, x);
}
return;
}
int main_path[MAXN];
vector <int> path;
int twig[MAXN];
int rek(int x, int par) {
int ma = 0;
for (int y : ve[x]) {
if (y == par) continue;
if (main_path[y]) continue;
ma = max(ma, rek(y, x));
}
if (ma == 3) impossible();
twig[x] = ma;
return ma + 1;
}
vector <int> out;
void print() {
cout << "YES\n";
cout << out.size() << "\n";
for (int x : out) cout << x + 1 << " ";
cout << "\n";
return;
}
int main() {
int n, m;
cin >> n >> m;
if (n == 1) {
out.push_back(0);
print();
return 0;
}
if (n == 2) {
out.push_back(0);
out.push_back(0);
print();
return 0;
}
REP(i, m) {
int a, b;
cin >> a >> b;
a--, b--;
ve[a].push_back(b);
ve[b].push_back(a);
}
dfs(0, 0);
int A = -1, dist = -1;
REP(i, n) {
if (bio[i] > dist) {
dist = bio[i];
A = i;
}
}
memset(bio, 0, sizeof bio);
dfs(A, A);
int B = -1;
dist = -1;
REP(i, n) {
if (bio[i] > dist) {
dist = bio[i];
B = i;
}
}
int x = B;
while (x != A) {
main_path[x] = 1;
path.push_back(x);
for (int y : ve[x]) {
if (bio[y] == bio[x] - 1) {
x = y;
break;
}
}
}
path.push_back(A);
main_path[A] = 1;
memset(twig, 0, sizeof twig);
REP(i, n) {
if (main_path[i]) twig[i] = rek(i, i) - 1;
}
// remove first and last node of path to optimise
if (path.size() > 1) {
main_path[path[0]] = 0;
path.erase(path.begin());
twig[path[0]] = max(twig[path[0]], 1);
}
reverse(path.begin(), path.end());
if (path.size() > 1) {
main_path[path[0]] = 0;
path.erase(path.begin());
twig[path[0]] = max(twig[path[0]], 1);
}
for (int x : path) {
out.push_back(x);
if (twig[x] == 2) {
for (int y : ve[x]) {
if (main_path[y] || twig[y] == 0) continue;
out.push_back(y);
out.push_back(x);
}
}
}
reverse(path.begin(), path.end());
for (int x : path) {
out.push_back(x);
if (twig[x] == 2) {
for (int y : ve[x]) {
if (main_path[y] || twig[y] == 0) continue;
out.push_back(y);
out.push_back(x);
}
}
}
print();
return 0;
}