题意
在 $\left[1, 2000\right]$ 中选若干个数,求有多少种方法使得它们的和是 $5$ 的倍数?
题解
首先,可以猜测答案差不多是 $\dfrac15 \cdot 2^{2000}$,因为 $5$ 种选法里平均会有 $1$ 种满足要求。
但是 $\dfrac15 \cdot 2^{2000}$ 这个东西并不是一个整数,说明答案肯定跟它有一定差距。
现在,我们使用生成函数来描述我们的选法。
$$F\left(x\right) = \prod\limits_{i = 1}^{2000} \left(1 + x^i\right)$$
考虑这样有什么性质。如果不选一个数,那么可以看作乘了个 $1$,而选一个数 $i$,则可以看作乘了 $x^i$。
那么最后的和是什么呢?把所有选的数加起来就是和,而 $x^i \cdot x^j = x^{i + j}$,刚好可以表示。
所以,最终我们的答案就是所有指数是 $5$ 的倍数的项的系数之和了。
$F$ 函数现在还有另一种写法:
$$F\left(x\right) = \sum\limits_s c_s x^s = c_0 + c_1x + c_2x^2 + c_3x^3 + \cdots$$
现在,考虑把一些特殊值代入 $F$ 函数。
$$ \begin{aligned} F\left(0\right) &= 1^{2000} = c_0\\ F\left(1\right) &= 2^{2000} = c_0 + c_1 + c_2 + \cdots\\ F\left(-1\right) &= 0 = c_0 - c_1 + c_2 - c_3 + \cdots \\ \frac12\left(F\left(1\right) + F\left(-1\right)\right) &= 2^{1999} = c_0 + c_2 + c_4 + c_6 + \cdots \end{aligned} $$
这样,我们得到了所有指数是 $2$ 的倍数的项的系数之和。
有没有可能用类似的方法得到所有指数是 $5$ 的倍数的项的系数之和呢?
我们可以把这种正负颠倒看作一条射线绕原点旋转,每次旋转 $180$ 度,那有没有可能让它旋转 $5$ 次回到原来的方向,每次旋转 $72$ 度?
考虑 $z^5 = 1$ 这个方程在复数域内的解。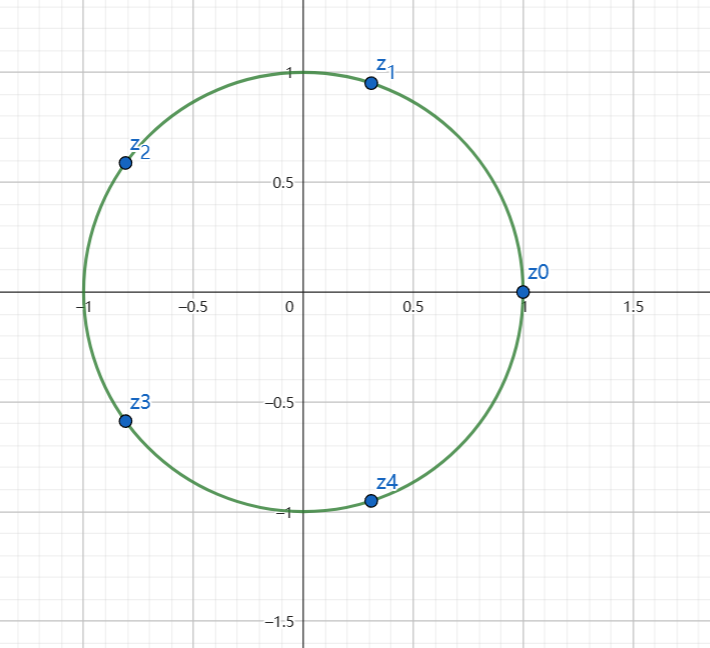
这些解会形成一个圆,而我们取距离相等的 $5$ 个点,方便后续操作。
那么,现在答案就是
$$\frac15\sum\limits_{i=0}^4 F\left(z_i\right)$$
考虑如何计算 $F\left(z_i\right)$。
我们知道这些 ${z_i}^j$ 的意义:这相当于是在单位圆上转圈。所以其实只需要管 ${z_i}^{j \bmod 5}$ 就行。
知道了这个之后,我们来看看 $F\left(z_1\right)$ 怎么算。
我们知道,
$$F\left(x\right) = \prod\limits_{i = 1}^{2000} \left(1 + x^i\right)$$
而因为 ${z_i}^j = {z_i}^{j \bmod 5}$,所以
$$F\left(z_1\right) = \left(\prod\limits_{i = 1}^{5} \left(1 + {z_1}^i\right)\right)^{400}$$
注意到:$k^5 - 1 = \left(k - {z_1}^0\right)\left(k - {z_1}^1\right)\left(k - {z_1}^2\right)\left(k - {z_1}^3\right)\left(k - {z_1}^4\right)$
所以,代入 $k = -1$,$\left(-1\right)^5 - 1 = \left(-1 - {z_1}^0\right)\left(-1 - {z_1}^1\right)\left(-1 - {z_1}^2\right)\left(-1 - {z_1}^3\right)\left(-1 - {z_1}^4\right)$
刚好是我们要求的东西的相反数。
因此 $F\left(z_1\right) = 2^{400}$
同样的道理,$F\left(z_2\right) = F\left(z_3\right) = F\left(z_4\right) = 2^{400}$。
而因为 $z_0 = 1$,所以 $F\left(z_0\right) = 2^{2000}$。
因此
$$\frac15\sum\limits_{i=0}^4 F\left(z_i\right) = \frac15\left(2^{2000} + 4 \cdot 2^{400}\right)$$
这个东西确实很接近 $\dfrac15 \cdot 2^{2000}$。
其实这种使用复数单位圆的思想并不稀有。
参考
https://www.youtube.com/watch?v=bOXCLR3Wric